【西瓜书】第十章 降维与度量学习
本文是周志华老师《机器学习》第十章降维与度量学习的学习笔记
k近邻学习
k近邻学习是一种常用的监督学习方法, 工作的机制非常简单,对于每个给定的测试样本, 基于某种距离找出训练集中与其最相近的k个训练样本, 然后基于这些邻居的信息来预测该测试样本. 在分类任务中,可以采取投票法, 在回归任务中可以采取平均法, 更复杂一些也可以采取各种加权方式.
显然可以看出, k近邻方法没有显式的训练过程, 它是懒惰学习的著名达标,训练时间开销为零.
k近邻学习中两个重要的点:
- k的选取
- 距离的定义
假设我们固定住第二点, 并设$k=1$, 来讨论一些这种最近邻分类器在二分类问题上的性能. 此时我们给定测试样本$x$, 并设其最邻近样本为$z$, 则容易得出分类器出错概率为:
假设样本独立同分布, 且对任意$x$和任意小正数$\delta$, 在$x$附近$\delta$距离范围内总能找到一个训练样本. 令$c^*=arg \max_{c\in Y}P(c|x)$表示贝叶斯最有分类器的结果, 则可以推导出:
这表示最近邻分类器的泛化错误率不超过贝叶斯最有分类器错误率的两倍.
低维嵌入
前面的讨论基于一个假设: 对任意$x$和任意小正数$\delta$, 在$x$附近$\delta$距离范围内总能找到一个训练样本. 但是遗憾的是现实中很难满足这种情况, 且随着特征维数的增长, 所需要的样本数会飞速增长, 且高维特征也会使得距离运算更加耗时.
这种在高维情况下出现的样本稀疏, 计算困难等问题, 是许多ML方法都面临的共同问题,称为维数灾难.
缓解维数灾难的一种方法就是降维, 又称维数约简, 即将原始高维属性空间转变成一个低维子空间.
降维的依据在于, 虽然数据样本是高维的,但是与学习任务密切相关的也许仅仅是某个低维分布.
MDS多维缩放
一种很经典的降维方法叫做”多维缩放”(Multiple Dimensional Scaling, MDS), 能够将原始空间中样本之间的距离在低维空间中保持.
假设$m$个样本在原始空间的距离矩阵为$D\in \mathbb{R}^{m\times m}$, 其中第$i$行第$j$列的元素$d_{ij}$为两个样本之间的距离. 那么我们的目标就是获得样本在$d’$维空间的表示 $Z\in \mathbb{R}^{d’\times m}, d’\le d$, 且任意两个样本在$d’$维空间中的欧氏距离等于原始空间中的距离,即$||z_i-z_j||=d_{ij}$.
令 $B=Z^TZ\in \mathbb{R}^{m\times m}$, 其中$B$为降维后样本的内积矩阵, $b_{ij}=z_i^T$, 那么有:
为了简化推导, 假设我们已经中心化了样本$Z$, 则推导后可以得到:
由此可以利用降维前的距离矩阵$D$来求降维后的内积矩阵$B$, 并对其做特征值分解$B=V\Lambda V^T$, 其中$\Lambda$ 为特征值组成的对角矩阵, $V$为特征向量矩阵. 假设其中有$d$个非零特征值, 它们组成的对角矩阵$\Lambda$和特征向量矩阵$V*$则有以下关系:
实际中, 为了有效降维(降到$d’$), 则不一定要求降维后的距离严格相等, 此时取前$d’$个非零特征值对应的$\tilde{\Lambda}$和$\tilde{V}$:
除了MDS, 线性变换降维是最简单的降维方法, 这类方法被称作线性降维方法, 例如下面要介绍的PCA主成分分析.
主成分分析
主成分分析(Principal components analysis, PCA),在模式识别里面还有个名字叫KL变换(虽然二者有细微的不同)。
它是一种常用的降维方法,由最大可分性(样本点在该超平面上的投影尽可能分开,即最大化投影方差,同时这也是最小化均值误差)。
PCA分析属于一种正交变换,即,将原始特征做正交变换,获得的每个特征都是原特征的线性组合,然后从中选出部分特征,作为变换的输出。
假设我们的样本数据都做了均值归一化,那么所有样本点投影后的方差就是$\sum W^Txx^TW$, 其中$W$是变换矩阵。 那么,优化的目标就是:
对上式用拉格朗日乘子法得到:
那么,对协方差矩阵$XX^T$做特征值分解,将求得的特征值排序,取前$d’$个特征值构成的特征向量构成$W$,就得到PCA的解,维数由$d$降到了$d’$。 这里的$d’$值可以人工指定,也可以通过其他开销小的学习器来交叉验证。或者通过重构阈值来设定,例如设$t=95%$,选择合适的$d’$使得
当然,降维不可避免地会丢失一些信息,但是样本有用信息的密度增大,同时也会一定程度的降噪,从信息论的角度来说,数据的信噪比提高了。
然而,需要注意的是, PCA在分类领域往往起到的作用很小,因为虽然它保留了大部分的信息,但是被它抛弃的可能往往是那些能够起到区分作用的信息,例如,字符识别中的O和Q,PCA很可能会丢去掉右下角那个“尾巴”的特征。适当留意它和LDA线性判别的区别,二者一个是寻找能够最大保留信息的主轴方向,一个是用来寻找最有效分类的方向。
另外, 我们这里可以看到, PCA对协方差矩阵$XX^T$做特征分解, 前面的MDS可以看做是对$X^TX$(内积)做特征分解, 因此二者互为对偶方法.
核化线性降维
现实任务中,可能会需要非线性映射才能找到合适的低维嵌入,进行非线性降维的常用方法是基于核技巧来对线性降维方法进行核化.
书中给出了核化主成分分析算法(KKPC)
流形学习
流形学习是一类借鉴了拓扑流形概念的将为方法.
流形是在局部与欧式空间同胚的空间, 即它在局部具有欧式空间的性质并能用欧氏距离来计算距离.
下面介绍两种流形学习的方法.
等度量映射 Isomap
等度量映射(Isometric Mapping, Isomap)的出发点在于, 低维流形嵌入到高维空间后, 直接在高维空间计算直线距离有误导性. 举个例子, 假设一个一维直线的流形, 嵌入到二维空间中, 变成一个类似字母”C”的样式, 那么原来直线两端点就变成C的两个端点, 在原来的一维空间中二者的距离(测地线)是很长的, 但是由于嵌入到高维时弯曲了, 因此在高维空间中计算二点距离就小了很多, 此时该距离和我们要求的测地线就有了很大的偏差.
为了解决该问题, Isomap利用近邻点来计算两点距离,那么计算测地线距离的问题就转变为计算近邻接图上两点的最短路径问题(该问题可以用Dijkstra或者Floyed算法解决), 得到任意两点距离后, 就可以通过前面的MDS算法来获得样本点在低维空间的坐标.
具体算法如下: Isomap算法
Isomap算法
这里需要注意的是, Isomap仅仅得到了训练样本在低维空间的坐标, 但是对于新样本, 如何进行映射呢, 一种常用的做法是训练一个基于训练样本高维坐标和低维左边的回归器, 并应用于新数据. 当然这么做只是一个权宜之计, 但是目前并没有更好的方法.
最近邻图的构建有两种方法:
- 指定近邻点个数$k$, 连接最近的$k$个点作为近邻点
- 制定距离阈值$\varepsilon$, 距离小于该阈值的点作为近邻点
当近邻范围过大, 则距离很远的点也可能会被误认为近邻, 从而出现短路问题; 当范围过小, 则图中有些区域和其他区域可能不存在连接, 则出现断路问题.
局部线性嵌入 LLE
局部线性嵌入(Locally Linear Embedding)假设样本点能够通过它的领域样本$x_j, x_k, x_l$的坐标通过线性组合重构而来, 即:
LLE希望这个性质能在低维空间中得以保持. 那么对于每个$x_i$, LLE会根据近邻样本计算出线性重构的系数$w_i$ (拉格朗日乘子法).
然后该性质在低维空间保持$w_i$不变, 接着就要确认$x_i$对应的低维空间坐标$z_i$, 通过前面算出来的$w$组成的$W$,令:
接着, 对$M$做特征值分解, 最小的$d’$个特征值对应的特征向量就组成了$Z^T$. 具体推导过程就不赘述了,那么LLE算法就可以描述如下: LLE算法
LLE算法
显然, 对于任何$x$, 不在其邻域内的变动都不会对$x$及其对应的$z$产生影响,这种将变动限制在局部的思想在很多方法都有用.
度量学习
之前的降维可以看做是寻找一个合适的距离度量所在的低维空间, 那么我们也可以在原空间中寻找这样一个距离度量, 这也是度量学习metric learning的基本动机.
我们这里就需要一个可以调节的参数来对度量进行学习, 对于欧式空间而言, 其平方距离可以写作:
我们设定每个属性的权重为$w$, 权重矩阵即为$W$, 那么重新定义距离:
其中$W$是一个对角矩阵. 此时我们可以通过学习来确定$W$.
更进一步的, 我们取消$W$的对角矩阵限制(即属性之间无关, 互相正交的假设), 令其为一个半正定矩阵$M$, 于是就得到了马氏距离:
其中$M$就叫做度量矩阵, 为了保证距离的非负和对称, 它必须是一个(半)正定对称矩阵, 即$M$可以以正交基的形式重写为$M=PP^T$.
下面我们以近邻成分分析为例来介绍如何学习$M$.
近邻成分分析 NCA
近邻成分分析 (Neighbourhood Component Analysis), 是一种近邻类分类器.
我们将近邻分类器在判别时进行的多数投票法换为概率投票法, 对于任意样本 $x_j$,它对$x_i$分类结果影响的概率(概率由样本间距离决定)为:
假设以留一正确率作为最大化, 即计算样本除了被自身以外所有样本正确分类的概率:
其中$\Omega_i$表示和$x_i$属于相同类别的样本的下标集合, 则整个样本集上留一法正确率为:
最后代入可以得到NCA总的优化目标为:
可以用梯度下降求解出度量矩阵$M$.
此外, 除了用监督学习的错误率作为优化目标, 可以引入领域知识, 利用pair-wise的必连/勿连约束来优化.
最后用一张图来汇总一些降维方法:
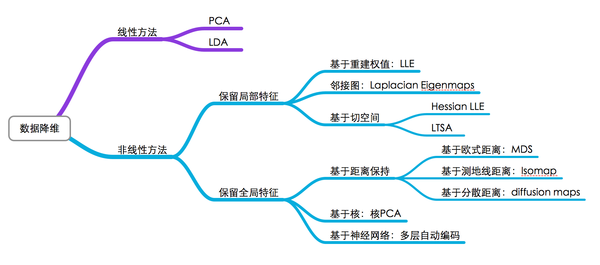
习题及参考答案
10.1 编程实现k近邻分类器, 在西瓜数据集3.0a上比较其分类边界与决策树分类边界的异同.
代码参见这里, 可以看到(一般)决策树的决策边界比较横平竖直,较为规整, K近邻的边界则不然, 且不同的k取值对结果有较大影响.
10.2 令$err$, $err*$分别表示最近邻分类器与贝叶斯最优分类器的期望错误率, 试证明:
略, 书中p226页旁注有提到证明参考.
10.3 在对高维数据降维之前应先进行”中心化”, 常见的是将协方差矩阵$XX^T$转为$XHH^TX^T$,其中$H=I-\frac{1}{m}11^T$,试分析其效果
(题目似乎有些问题, 1矩阵应该一个就够了即$11^T$应为$1$)
这里很简单:
其中$\hat{X}$ 为$X$的行均值, 这样$XH$的均值就被转换到了原点.
10.4 在实践中, 协方差矩阵$XX^T$的特征值分解常用中心化后的样本矩阵$X$的奇异值分解代替, 试述其原因.
首先求协方差矩阵之前也需要对数据进行中心化得到$X$.
对$X$做奇异值分解, 即求$X=U\Sigma V^T$, 其中$U$就是$XX^T$的特征向量, $V$是$X^TX$的特征向量, 因此也得到了特征向量.
至于为什么常用SVD来替代特征值分解, 这里有较为详细的阐述, 总结起来无外乎是SVD的数值精度更高,因为计算$XX^T$的平方运算会导致一些精度损失.
10.5 降维中涉及的投影矩阵通常要求是正交的,试述正交,非正交投影矩阵用于降维的优缺点.
就不分开表述了, 正交和非正交的优缺点刚好是反着来的. 直接谈正交吧.
首先啥叫正交呢, 简单说就是两向量互相”垂直”, 内积为0.
使用正交投影矩阵的优点在于计算简便, 对于正交基而言, 计算线性组合权值更加方便了(因为正交基内各向量线性无关性), 在降维中正交投影时, 正交投影矩阵还满足 最佳逼近定理.
但是缺点也比较明显(不确定哈..), 如果降维时丢弃的维度的特征就彻底不存在了,因为线性无关的缘故, 丢弃的维度无法通过其他维度基的线性组合来表示,因此当正交基有较为有用的实际含义时会有一些问题?
10.6 使用MATLAB中的PCA函数对Yale人脸数据集进行降维,并观察前20个特征向量所对应的图像.
这里sklearn上有一篇文章有所描述,且将PCA和其他方法做了对比, 值得一看, 传送门.
10.7 试述核化线性降维和流形学习之间的联系和优缺点.
首先二者都是非线性降维, 前者是基于核的,后者流形学习往往是利用了局部性, 例如LLE利用局部性来对样本做重表征,Isomap利用局部性构建测地线距离再加上MDS(注意二者利用局部性的不同).
流形学习一般被认为对outlier和噪声比较敏感, 而核化线性降维的比较难以兼顾泛化性和效率.
10.8 $k$近邻图和$\varepsilon$近邻图存在的短路和断路问题会给Isomap造成困扰,试设计一个方法缓解该问题.
想到两种方法:
- 把两种构图方法结合一下, 当距离小于$\varepsilon$范围内有近邻点时设定其最近的点为近邻点.
- 当发生短路时,在近邻范围内启发式人为增加样本(例如增加指定点和其最近邻的中点),当然这么做会改变样本分布, 当数据很稀疏时不能这么玩.
10.9 试设计一个方法为新样本找到LLE降维后的低维坐标
首先对新样本在训练集中确定其$k$近邻, 由于LLE假设了局部性, 所以只要利用这$k+1$个数据来做接下来的LLE算法运算而不用重新计算整个数据集.
10.10 试述如何确保度量学习产生的距离能满足距离度量的四条基本性质.
- 非负性 $d\ge 0$
- 同一性 $d_{ij}=0$当且仅当$i=j$
- 对称性 $d_{ij}=d_{ji}$
- 直递性 $d_{ij}\le d_{ik}+d_{kj}$







