【西瓜书】第十二章 计算学习理论

　基础知识　　

计算学习理论是机器学习的理论基础，其目的是分析学习任务的困难本质，并根据分析结果指导算法设计．　　
Coursera上有一门很热门的台湾课程<机器学习基石>, 其上半部分都是在讲这部分内容, 足见其重要性.

我们给定数据集 $D={x,y}$, 假设所有样本$x \in \mathcal{X} y \in \mathcal{Y}$独立同分布,并服从分布$\mathcal{D}$.
$h$为$\mathcal{X \rightarrow Y}$的映射, 泛化误差为:

$$E(h;\mathcal{D})=P(h(x)\neq y)$$

$h$在$D$上的经验误差为:

$$\hat{E}(h;D)=\frac{1}{m}\sum(h(x)\neq y)$$

那么由于独立同分布, 经验误差的期望等于泛化误差, 学习理论非常关注的一个点在于经验误差的上限, 我们记作$\epsilon$ ,以及经验误差和泛化误差的逼近程度.
如果h在数据集D上经验误差为0, 则称二者一致, 否则称为不一致. 我们通过”不合”(disagreement)来度量两个映射之间的差别:

$$d(h_1, h_2) = P(h_1(x) \neq h_2(x))$$

下面是一些在推导中经常用到的不等式:

1. Jensen 不等式： $$f ( \mathbb { E } ( x ) ) \leqslant \mathbb { E } ( f ( x ) )$$

1. Hoeffding不等式, 对$m$个随机变量$x_1, …, x_m$， $0\le x_i \le 1$, 则对任意$\epsilon \gt 0$ $$P \left( \frac { 1 } { m } \sum _ { i = 1 } ^ { m } x _ { i } - \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \mathbb { E } \left( x _ { i } \right) \geqslant \epsilon \right) \leqslant \exp \left( - 2 m \epsilon ^ { 2 } \right)$$

$$P \left( \left| \frac { 1 } { m } \sum _ { i = 1 } ^ { m } x _ { i } - \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \mathbb { E } \left( x _ { i } \right) \right| \geqslant \epsilon \right) \leqslant 2 \exp \left( - 2 m \epsilon ^ { 2 } \right)$$

1. McDiarmid不等式，对任意$1\le i\le m$，函数$f$满足：

$$\sup _ { x _ { 1 } , \ldots , x _ { m } ^ { \prime } } \left| f \left( x _ { 1 } , \ldots , x _ { m } \right) - f \left( x _ { 1 } , \ldots , x _ { i - 1 } , x _ { i } ^ { \prime } , x _ { i + 1 } , \ldots , x _ { m } \right) \right| \leqslant c _ { i }$$

则对任意$\epsilon \gt 0$ 有：

$$P \left( f \left( x _ { 1 } , \ldots , x _ { m } \right) - \mathbb { E } \left( f \left( x _ { 1 } , \ldots , x _ { m } \right) \right) \geqslant \epsilon \right) \leqslant \exp \left( \frac { - 2 \epsilon ^ { 2 } } { \sum _ { i } c _ { i } ^ { 2 } } \right)$$ $$P \left( \left| f \left( x _ { 1 } , \ldots , x _ { m } \right) - \mathbb { E } \left( f \left( x _ { 1 } , \ldots , x _ { m } \right) \right) \right| \geqslant \epsilon \right) \leqslant 2 \exp \left( \frac { - 2 \epsilon ^ { 2 } } { \sum _ { i } c _ { i } ^ { 2 } } \right)$$

PAC学习

PAC理论(概率近似正确 Probably Approximately Correct)是学习理论中最基本的理论.
为了介绍该理论需要引入一些定义:

• $c$表示概念(concept), 表示样本空间到标记空间的映射, 若有对任何样例$(x,y)$有$C(x)=y$,则称$c$为目标概念, 所有目标概念的集合称为概念类$\mathcal{C}$
• $\mathcal{L}$为学习算法, 其能表示的所有可能概念的集合称为假设空间, 用$\mathcal{H}$表示. 由于$\mathcal{H},\mathcal{C}$通常不同, 所以对于$h\in \mathcal{H}$我们不确定其是否为目标概念,则称之为假设.
• 若假设空间存在至少一个目标概念, 则称该问题对算法$\mathcal{L}$可分,一致, 否则即为不可分,不一致.

那么显然, 我们希望学习算法学到的h尽可能接近c(准确学到c太难),换言之,我们希望以较大的概率学到误差满足预设上限的模型, 也就是”概率” “近似正确”的含义.
我们定义PAC辨识: 对$0\lt \epsilon$, $\delta \lt 1$, 所有$c\in \mathcal{C}$和分布$\mathcal{D}$, 若存在学习算法$\mathcal{L}$, 其输出的假设$h\in \mathcal{H}$ 满足:

$$P(E(h)\le \epsilon)\ge 1-\delta$$ 则称该算法能从假设空间中PAC辨识概念类. 这种算法能够以至少$1-\delta$的概率学到和目标概念误差最多为$\epsilon$的近似. 在此基础上可以定义PAC可学习:  显然, 相对于PAC辨识, PAC可学习加强了**对样本数的限制**, 一个好的学习算法当然是应该能够利用较少的样本就达到目的. 进一步的我们来定义**PAC学习算法**  这里我们在PAC可学习的基础上加上了对时间复杂度的限制, 不可能任由一个算法跑到地老天荒不是. 如果我们假设学习算法处理每个样本的时间为常数, 那么上述的时间复杂度就可以归结为样本复杂度:  PAC学习中一个重要因素在假设空间$\mathcal{H}$的复杂度, 假设空间包含了算法所有可能输出的假设.若假设空间和概念类完全相同$\mathcal{H= C}$, 即为"恰Pc可学习", 社意味着算法的学习能力和学习任务恰好匹配. 当然,这种情况基本上很难存在, 所以我们往往希望假设空间越大, 这样它包含目标概念的概率也越大, 不过NFL, 这时从中搜索寻目标概念的难度也越大. 下面分有限和无限两种情况讨论. ## 有限假设空间 ### 可分情况 此时, 目标概念数据假设空间, 那么有一种很简单的策略, 既然$\mathcal{H}$中包含目标概念$c$, 那么任何在D上出现错误的假设都不可能是目标概念, 则将其剔除, 如果数据集足够大, 那么我们就能够将$c$筛选出来. 但是如果数据集不够大, 我们就有不止一个与D一致的等效假设了. 下面我们来看看究竟需要多少数据才能学到目标概念的近似呢? 经过简单的推导, 我们可以得出 $$m\ge \frac{1}{\epsilon}(ln|\mathcal{H}|+ln\frac{1}{\delta})$$

因此我们可以得到有限假设空间都是PAC可学习的.

不可分情况

此时目标概念$c$不存在于假设空间中, 我们可以证明:

$$P(|E(h) - \hat{E}(h)|)\le \sqrt{\frac{ln|\mathcal{H}|+ln(2/\delta)}{2m}}\le 1-\delta$$

可以看出, 我们虽然没有办法学到目标概念,但是肯定可以学到一个泛化误差最小的假设, 如此,我们就将PAC学习推广到$c\notin \mathcal{H}$的情况, 也就是不可知学习.

VC维

但是现实中我们通常面临的都是无限假设空间, 这是我们常用的工具就是假设空间的VC维.

我们先来讨论几个概念:

1. 增长函数
   对于假设$h$, 我们用它来对样本集赋予标记, 可以得到 $$h|_D={(h(x_1), h(x_2),...,h(x_m))}$$ 随着$m$ 增大, 假设空间中所有假设对D中样本所能赋予的标记数的可能结果也会增加. 我们定义增长函数为: $$\Pi_{\mathcal{H}}(m)=max|{(h(x_1),h(x_2),...,h(x_m))|h\in \mathcal{H}}|$$ 也就是假设空间对样本集所能赋予标记的最大可能结果数. 增长函数能够体现假设空间的表达能力和复杂度, 有定理如下: $$P(|E(h) - \hat{E}(h)|\gt \epsilon)\le4\Pi_{\mathcal{H}}(2m)exp(-\frac{m\epsilon^2}{8})$$
2. 打散
   如果假设空间能够实现数据集上所有”对分”(我们称假设对数据集中数据赋予标记的每种可能结果称作对分), 对于二分类问题即为增长函数为$2^m$, 则称示例集能被假设空间打散.

下面就可以开始讨论VC维了,假设空间的VC维是能被$\mathcal{H}$打散的最大示例集的大小,即:

$$VC(\mathcal{H})=max \{ m: \Pi_{\mathcal{H}}=2^m\}$$

这里需要注意$VC(H)=d$表示存在大小为$d$的示例集能被打散,但不代表所有大小为d的示例集都能被打散. 可以看出VC维的定义和分布无关, 通常我们用大小为$d$的示例集能被打散, 而$d+1$的数据集不能来计算VC维.

那么显而易见的是VC维和增长函数应该会有密切的联系,有一个重要的引理, Sauer引理给出了二者之间的的定量关系(证明在西瓜书p275,数学归纳法, 还是比较漂亮的):

$$\Pi_{\mathcal{H}}\le\sum_{i=0}^dC^i_m$$

从而可以计算出增长函数的上界:

$$\Pi_{\mathcal{H}}\le (\frac{e\times m}{d}^d)$$

然后得到我们最终想要的基于VC维的泛化误差:

$$P(|E(h) -\hat{E}(h)|\le \sqrt{\frac{8dln\frac{2em}{d} + 8ln\frac{4}{\delta}}{m}}) \ge 1-\delta$$

那么可以发现,任何VC维有限的假设空间都是(不可知)PAC可学习的.
这给出了在无限假设空间中学到满足经验风险最小化(ERM原则 Empirical Risk Minimization)的算法的理论保证, 而且VC维给出了我们在选择算法时的一种评价标准, 这里借用林轩田老师在机器学习基石里的一张图:

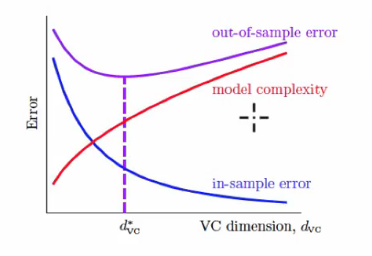
由于台湾和大陆术语上不太一致, 解释下这里的in-sample error就是经验误差, out-of sample error就是泛化误差. 可以发现, 不同VC维的算法, 如果VC维越高, 经验误差往往是能够持续下降的, 而模型复杂度也是上升的(很直观的看参数个数上升了嘛), 但是泛化误差会经历一个先下降后上升的过程, 其上升的过程即为我们熟知的过拟合. 那么, 如果能够从理论上分析出算法假设空间的VC维, 那就有助于我们设计和改进算法.

Rademacher 复杂度

之前提到基于VC维的泛化误差界是分布无关数据独立的，也就是说对任何数据分布都成立。 虽然这给VC维分析带来了普适性，但是这个往往会比较松。因此下面介绍一种考虑了数据分布的假设空间复杂度刻画方法。

这里不细谈了。

稳定性

这里算法稳定性考察的是算法在输入发生变化时，输出是否会随着发生变化。

我们在定义训练集的变化，$D$是来自分布$\mathcal{D}$的独立同分布采样数据集，对于假设空间$\mathcal{H}$,和学习算法$\mathfrak{L}$,令$\mathfrak{L}_ D\in \mathcal{H}$表示基于训练集从假设空间中学到的假设。 我们考虑以下的训练集变化：

• $D^{\backslash i}$表示移除第$i$个样本后的集合
• $D^i$表示替换第$i$个样本后的集合

接着我们定义以下损失函数：

• 泛化损失

  $$\ell ( \mathfrak { L } , \mathcal { D } ) = \mathbb { E } _ { \boldsymbol { x } \in \mathcal { X } , \boldsymbol { z } = ( \boldsymbol { x } , y ) } \left[ \ell \left( \mathfrak { L } _ { D } , \boldsymbol { z } \right) \right]$$

• 经验损失

$$\widehat { \ell } ( \mathfrak { L } , D ) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \ell \left( \mathfrak { L } _ { D } , \boldsymbol { z } _ { i } \right)$$

• 留一(leave-one-out)损失

$$\ell _ { l o o } ( \mathfrak { L } , D ) = \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \ell \left( \mathfrak { L } _ { D ^ { \backslash i } } , \boldsymbol { z } _ { i } \right)$$

接着定义算法的均匀稳定性：

定义 对任何 $x\in \mathcal{X}, z=(x,y)$，若学习算法$\mathfrak{L}$满足：

$$\left| \ell \left( \mathfrak { L } _ { D } , \boldsymbol { z } \right) - \ell \left( \mathfrak { L } _ { D ^ { | i } , \boldsymbol { z } } \right) \right| \leqslant \beta , i = 1,2 , \ldots , m$$

则成学习算法关于损失函数$\ell$满足$\beta-$均匀稳定性。

稳定性分析关注的是$| \widehat { \ell } ( \mathfrak { L } , D ) - \ell ( \mathfrak { L } , \mathcal { D } ) |$，而假设空间复杂度分析关心的是$\sup _ { h \in \mathcal { H } } | \widehat { E } ( h ) - E ( h ) |$.

稳定性和可学习性二者之间可以有下面的关系：
定理 若学习算法$\mathfrak{L}$是ERM且稳定的，则假设空间$\mathcal{H}$可学习。

这里的ERM指的是经验风险最小化（Empirical Risk Minimization），即学习算法输出的假设满足经验损失最小化。