线性代数要旨(二)
之前学习线性代数也刷了不少遍了,最近又频繁用到,发现理解的还是不够深,把之前写的笔记翻出来汇总一下。线性代数要旨(一)线性方程组/矩阵代数/行列式线性代数要旨(二)向量空间/特征向量/正交性/最小二乘法/二次型线性代数要旨(三)线代四大基本定理/可逆矩阵定理
ch4 向量空间 ‘线性代数及其应用笔记’具体数学
ch4 向量空间 ‘线性代数及其应用笔记’
4.1 向量空间与子空间
4.2 零空间,列空间和线性变换
4.3 线性无关集和基
4.4 坐标系
4.5向量空间的维数
4.6秩
4.7 基的变换
4.9 马尔科夫链中的应用
心得拾遗
错题
4.1 向量空间与子空间向量空间
一个向量空间是有一些被称为向量的对象构成的非空集合V,在这个集合上定义两个运算,称为加法和标量乘法(标量取实数),服从以下法则,这些法则必须对所有向量u,v,w及所有标量c和d均成立。
1. u,v之和u+v仍在V中
2. u+v=v+u
3. (u+v)+w=u+(v+w)
4. V中存在一个零向量0,使u+0=u
5. 对V中每个向量u,存在V中向量-u,使 ...
我的工作流 2017
最近coding的环境和工具都稳定下来了,也暂时找到了一个较为舒服和高效的工作流,所以这里总结一下。总的来说,工作环境主要分为三类:
笔记本的Windows环境,这里我用的是联想的Miix 5 pro。这款产品应该是联想对标surface pro的,当时是看中了它的手写笔,压感貌似在彼时是最灵敏的(4096级),而且价格比surface低不少的情况下,cpu还比surfce新一代。3月份某个早晨我写的价格监控爬虫告诉我降了1000块。。于是果断下单,很开心的是第二天就涨回原价而且半年内都没有更大的优惠了。
实验室给的台式机,我给装了linux,发行版是国产的deepin OS,界面好看而且常用软件比较多(QQ/WeChat/Netease Music/Baidu Yun)
实验室的服务器,Cent OS
基本上第二类和第三类都比较雷同。
编辑器 Vim基本上在linux上,除了markdown文件外,我都会使用vim了,在读了Practical Vim的一部分以及备受煎熬的刻意练习后,真是体会到了vim的畅快,虽然离:
用思考的速度编辑
...
【西瓜书】第十五章 规则学习
本文是周志华老师《机器学习》第十五章规则学习的学习笔记及部分习题答案。
规则: 语义明确,能描述数据分布所隐含的客观规律或领域概念的逻辑规则。形式化地看,规则形如:
\oplus\gets f_1\land f_2 \cdots f_L其中右边称作规则体(body),左边称作规则头(head)。可以看出,规则体是由逻辑文字组成的合取式。相较其他黑箱模型,规则学习有着以下优势:
良好的可解释性
极强的表达能力,便于引入领域知识
处理一些高度复杂的AI任务时有优势
对于规则,我们可以将其视作一个子模型,而规则集合就可以看作是集成模型。若一个样本满足一条规则,我们称之为被覆盖,那么我们需要规则集能够覆盖尽可能多的样例。
当每条样本被规则判定为不同结果时,我们称之为冲突,消解冲突往往用以下方法:
投票法:判别最多的类别作为最终规则
排序法:生成规则时就设定好规则的优先级
元规则:设定关于规则的规则,如“发生冲突时使用长度最小的规则”
规则可以分为两类:命题规则 : 由原子命题和逻辑连接词构成的简单陈述句一阶规则: 又称关系型规则,描 ...
【PRML】Lagrange Mulitiplier 拉格朗日乘子法
1234分页: 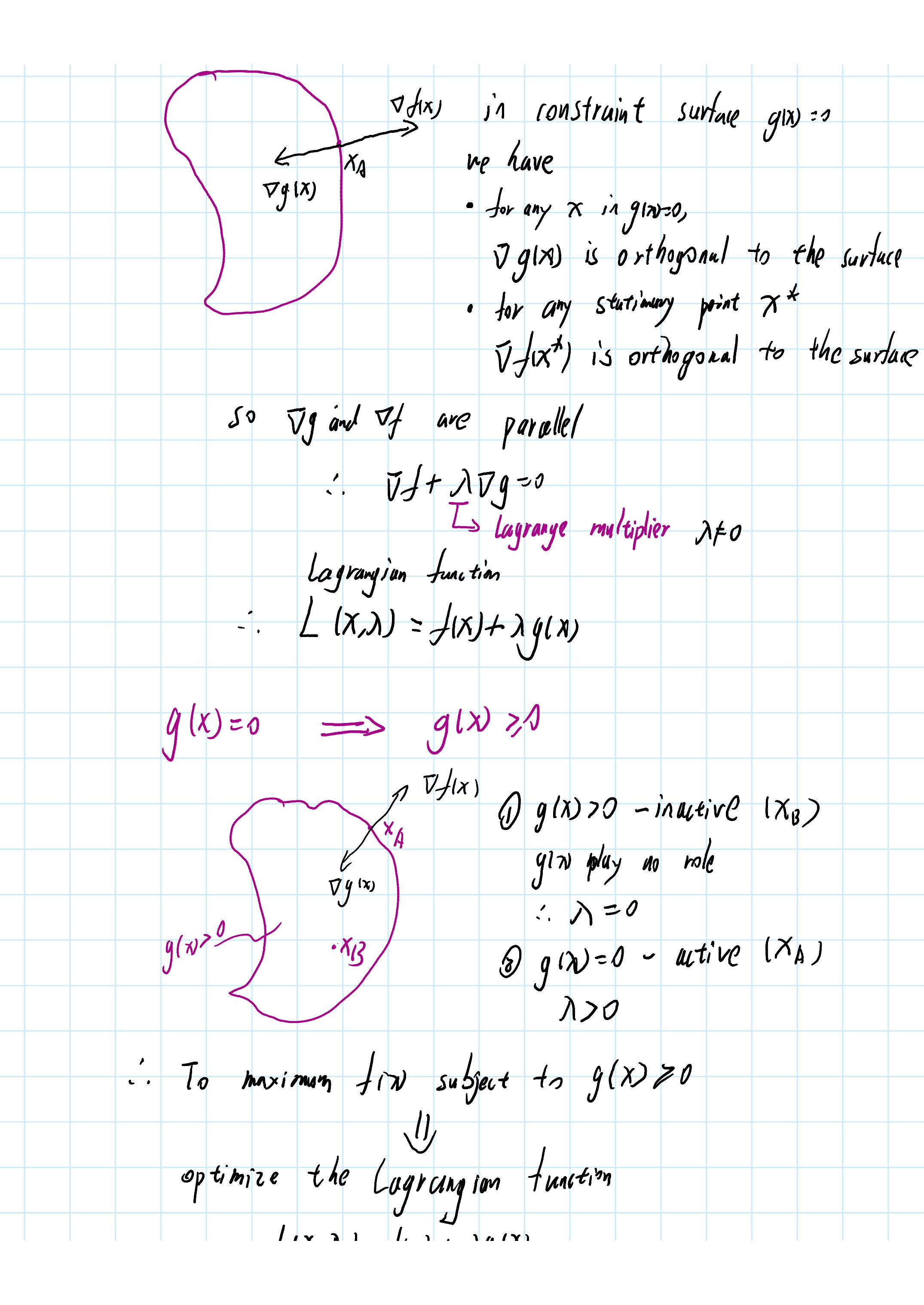
【西瓜书】第三章 线性模型
本文是周志华老师《机器学习》第三章线性模型的学习笔记。
基本形式f(x)=w^Tw+b其中 $w=(w_1;w_2;…;w_n)$线性模型简单,易于建模,可解释性好。
线性回归根据线性模型基本形式,我们也就是要求适当的 $w,b$ 使得其越接近真实的 $y$。这里我们用均方误差来度量性能,那么就有:
(w',b')=\underset{(w,b)}{arg\ min}\sum_{i+1}^m(y_i-wx_i-b)^2基于最小化均方误差来求解模型的方法叫做最小二乘法(least square method)。下面我们讨论一下一般情况下(样本由d个属性描述)的最小二乘法估计 $w,b$ 的做法。首先我们令 $\hat{w}=(w;b)$,同样的,将数据集表示为一个 $m\times(d+1)$ 大小的矩阵 $X$,每行对于一个样本,最后一个元素恒为1,那么就有:
\hat{w}'=\underset{\hat{w}}{arg\ min}(y-X\hat{w})^T(y-X\hat{w})令 $E_{\hat{w}}=(y-X\hat{w})^T(y-X\hat{w} ...
【西瓜书】 第七章 贝叶斯分类器
本文是周志华老师《机器学习》第七章贝叶斯分类器的学习笔记。 贝叶斯和频率学派的区别,一图以蔽之。
贝叶斯决策论 一般的形式化描述(来自Pattern Classification):令${w_1,\dots,w_c}$ 表示有限的c个类别集 ${\alpha_1,\dots,\alpha_a }$ 表示有限的a中可能采取的行为集,风险函数 $\lambda(\alpha_i|w_j) $ 描述了类别状态为$w_j$ 时采取行动$\alpha_i$ 时的风险。 特征向量$x$ 表示一个$d$ 维随机变量。令$p(x|w_j) $ 表示x的状态条件概率密度函数。那么我们由贝叶斯公式得到:
P(w_j|x) = \frac{p(x|w_j)P(w_j)}{p(x)}用非正式的英文可表达为:
posterior = \frac{likelihood \times prior }{evidence}那么特定模式x下采取行为$\alpha_i$ 的损失就是:
R(\alpha_i|x) =\sum \lambda(\alpha_i|w_j)P(w_j|x)形式化的来讲, ...
ThinkStats 统计思维
Chap 7 Relationships between variablesVisualizationIn most cases, the simplest way to check a relationship between two variables is scatter plot(散点图).To get better visual effect, usually we could use jittering to reverse the effect of rounding off. To handle the problem of too much overlapping points, we can set the parameter of alpha to less than 1.0.
However, when the dataset is bigger, hexbin may be a better choice to show the relationship.
In addition to scatter plot, bin one variable ...
从动物到上帝 ——人类简史
最近读了以色列历史学家尤瓦尔赫拉利的《人类简史》,颇有感触,下面稍作记录与备忘。该书主要分成四个部分来阐述,分别是认知革命,农业革命,人类的聚合统一与科学革命,下面就不妨也从这四个角度来讲。
认知革命这一部分聚焦于为何在各个人种之中,包括东非的鲁道夫人,东亚的直立人,欧洲和西亚的尼安特人,只有智人这一人种脱颖而出,存活并发展至今。作者认为,开始于大约7万年前的“认知革命”功不可没。在漫长的历史长河中,智人一开始并没有表现出相较其他人种更优越的地方,虽然说基因决定了智人拥有相对更加庞大的大脑,但是这从100万年前到认知革命开始的7万年前的93万年间,大脑更像是劣势。它们占据的体积大, 消耗的能量也更大,使得智人的肌肉相对萎缩,同时也需要花费更多时间寻找食物。但是,长夜终尽,大脑的物理属性使得智人更加擅长于构建并愿意相信虚构的事物,也就是营造一个想象共同体。一开始这种想象可能是万物之灵,部落的守护神,到了现代,这种想象共同体变得更加庞大和精致,它可以是国家,可以是公司,也可以是所谓人权。于此,智人能够组织出更大,更有凝聚力的团体,并由此发展出了更高级的语言和更丰富的文化。然而 ...
【模式识别】 线性判别函数
线性判别函数/判定面对于“判别函数”,我们指的是由$x$ 的各个分量线性组合而成的函数:
g(x)=w^tx+w_0其中$w$为权向量, w_0为偏置项。
两类我们利用$g(x)=0$ 定义一个判定面,它能够将两类点的分开来。当$g(x)$ 是线性时,我们就称之为超平面,一般用$H$ 表示。不难发现$H$ 的法向量就是$w$ ,而其位置由w_0 确定。那么对于特征空间中任意一点,我们可以表示为:
x=x_p+r\frac{w}{||w||}x_p$$ 是$x$ 在$H$ 上的投影, 而$r$ 是相应的算术距离。
由于$w$ 是$H$ 的法向量, 所以$w$ 和$$x_p$$ 正交,那么$$g(x_p)=0$$, 所以我们有:
$$g(x)=w^t(x_p+r\frac{w}{||w||}) +w_0 = g(x_p) + r||w||=r||w||
【西瓜书】第八章 集成学习
本文是周志华老师《机器学习》第八章集成学习的学习笔记。
集成学习(ensemble learning)通过构建多个学习器来完成学习任务。一般来说,先产生一组个体学习器,再用某种策略将其结合。当个体学习器均为同种类型的学习器时(如全都是决策树),我们称该集成为同质集成,此时称个体学习器为基学习器;否则称该集成为异质集成。
对于集成学习效果的理论保证,有一个简单的分析:对于二分类问题,其真实函数为$f$ ,假定基分类器的错误为$\epsilon$ ,对于每个基分类器有:
P(h_i(x)\ne f(x))=\epsilon假设我们的集成策略为简单投票法(超过半数基分类器分类正确,集成结果就正确):
H(x)=sign(\sum_{i=1}^Th_i(x))则根据Hoeffding不等式,集成的错误率为:
P(H(x)\ne f(x))=\sum_{k=0}^{\lfloor{T/2}\rfloor}C_T^k(1-\epsilon)^k\epsilon^{T-k}\le e^{-\frac{1}{2}T(1-2\epsilon)^2}该式显示出,随着集成中个体分类 ...






