激活函数二三事
本篇主要来复习一下关于激活函数的一些知识,其中包括激活函数的定义,作用,发展历程以及不同激活函数的优缺点与适用范围。
什么是激活函数
激活函数(activation function)又称非线性映射函数或是隐藏单元,是神经网络中中最主要的组成部分之一。 “激活”这个名字来自于生物上的神经网络结构。 我们知道,人工神经网络最初是受到生物上的启发,设计出了神经元这种单位结构,在每个神经元中,需要一个“开关”来决定该神经元的信息是否会被传递到其相连的神经元去,这个“开关”在这里也就是激活函数。
那么为什么要设计这样一个激活函数呢?
我们举例来说,通常一个两层的简单的全连接神经网络(MLP)可以写成(省略偏置项):
其中$\sigma$为激活函数,$W$为参数,$x,y$分别为输入和输出。
如果我们将激活函数去掉,那么这个两层的MLP就变成$y=W_2W_1x$,显而易见的,这个两层的神经网络就退化为一个单层的线性网络。 如果没有激活函数的非线性来赋予神经网络表达能力,那么无论多少层的网络结构都可以用一个单层网络来代替。
除了引入非线性外,在神经网络的输出层,激活函数还担任将前一层的输出映射到最终预测结果的任务。例如,对于一个二分类问题,通常最终输出层的激活函数就是sigmoid函数,而多分类任务则往往对应softmax函数。
总结一下,激活函数的意义如下:
- 模拟生物神经元特性,接受输入后通过一个阈值模拟神经元的激活和兴奋并产生输出
- 为神经网络引入非线性,增强神经网络的表达能力
- 导出神经网络最后的结果(在输出层时)
各类激活函数
阶跃函数
前面提到,激活函数最初是为了模仿生物神经元的激活特性,那么很自然想到,我们就用一个简单的阈值来判断是否激活好了,比如大于0的话就是激活该神经元,否则即为未激活,即如下的阶跃函数:
但是这简单方法的缺点也是非常明显的。 首先它是不连续且不光滑的,这就导致在反向传播时这一层很难学习。 其次阶跃函数“非黑即白”的特性虽然可能最符合生物神经网络,但是实际中有时我们需要表达“20%被激活”这种概念,即我们需要一个模拟的激活值而非简单的“01”二值.
Sigmoid 函数
既然阶跃函数有许多不足,特别是不连续。那么我们找一个相近的但是既光滑又连续的函数来代替不就可以了。 由此许多人想到了sigmoid函数。
严格上来说sigmoid函数不是一个单独的函数,而是指满足“S型”曲线的函数族,但是我们通常就用其中最常用的logistic函数来代指sigmoid函数:
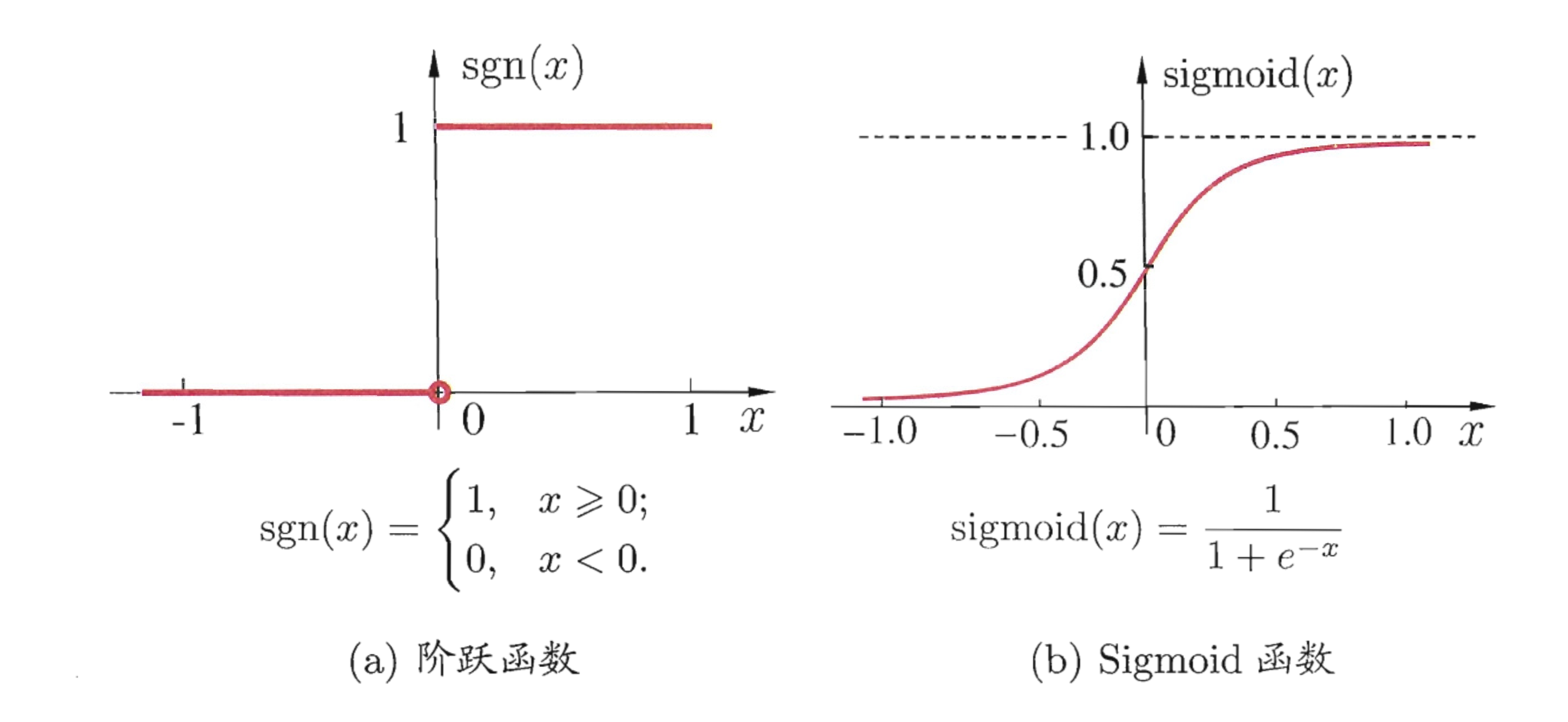
如图可以看出, sigmoid函数和阶跃函数非常相似,但是解决了光滑和连续的问题,同时它还成功引入了非线性。 由于其值域处在0~1,所以往往被用到二分类任务的输出层做概率预测。
那么这样一个函数是不是就完美了呢?
其实不然,简单观察就可以发现,当输入值大于3或者小于-3时,梯度就非常接近0了,在深层网络中,这非常容易造成“梯度消失”(也就是反向传播时误差难以传递到前面一层)而使得网络很难训练。此外,sigmoid函数的均值是0.5,但是不符合我们对神经网络内数值期望为0的设想。因而,人们提出了它的一个变种。
Tanh 函数
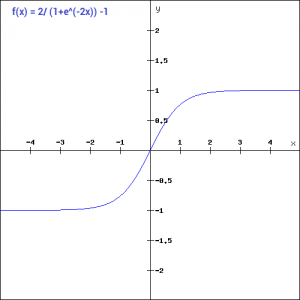
这个tanh函数又被称作双曲正切函数,可以看出它的函数范围是(-1,1)而均值为0,解决了上面sigmoid的一个问题。但是不难发现,该函数依旧没有解决梯度消失的问题。
Softplus 函数
softplus是sigmoid和tanh出现之后提出的一个替代方案,它的函数形式是:

很有趣的一点是,如果你对它求导,会发现它的导数就是是sigmoid函数。
这个函数它完成了对低于阈值部分的抑制(小于0)和大于0部分的激活。在两部分内都是可导的且梯度恒等,这就解决了梯度消失的问题(需要注意这里值域是零到正无穷,因此通常无法用于输出层)。当时softplus函数在反向传播时计算耗费较大,所以应用不是特别广。
ReLu 函数
ReLu函数(及其变种),又叫线性整流单元,应该说是当前最常用的一个激活函数了,尤其是在卷积神经网络和层次较深的神经网络中。
其函数形式很简单:
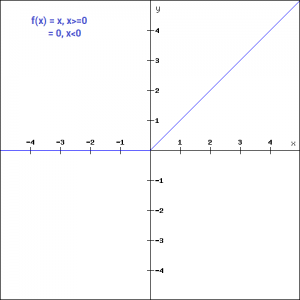
将其和softplus的图像比较,可以发现其实二者图形非常相似,不同点在于ReLu将$x=0$处的光滑曲线替换为了折现,这使得它的计算也相对更加简单,而且有助于随机梯度下降算法收敛(有研究指出收敛加速可达6倍)。当然ReLu函数也能够缓解梯度消失的问题。
当然,ReLu还是有一些缺陷的,对于小于0的这部分值,梯度会迅速降为0而不在影响网络训练。 这会造成部分神经元从来不被激活,也称作“死区”。 这也给了ReLu函数的变种很多发挥空间。
ReLu 变种
为什么把ReLu变种单独拿出来说呢? 因为它的变种实在是有点多,有的是具体以论文形式提出的,有的是在数据竞赛中应用的,夸张的说,出去上个厕所说不定就有人提出一个新的变种。 下面选择几个较有影响力的说一下。
Leaky ReLu
之前提到过死区的现象,为了缓解这种情况,有研究者将$x\le 0$部分调整为$f(x)=\alpha x$,其中$\alpha$一般设为一个较小的正数如0.01或0.001。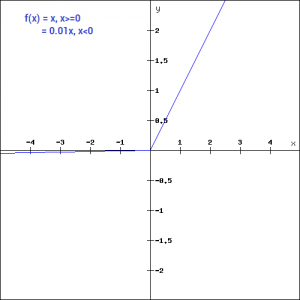
这样就将小于0部分的梯度从零提高到$\alpha$,给了这些被抑制部分一定参与网络训练的可能。当然原始的ReLu也可以看作是$\alpha=0$时的特例Leaky ReLu。
但是这里超参数$\alpha$很难去选定且较为敏感,因此实际性能并不稳定。
参数化 ReLu
参数化ReLu(Parameterised ReLu, PReLu)的形式和Leaky ReLu一样,唯一地不同是它将$\alpha$视作一个可训练的参数而不是人为设定的超参数。
这样,就避免了Leaky ReLu中的选定$\alpha$值的问题。
研究者发现,使用参数化ReLu能够较大提高网络性能,而且实验数据显示,随着网络深度的递增,$\alpha$值会减小,这样意味着网络需要的非线性能力随着深度递增而增加。在第一层网络时,参数化ReLu往往会学到一个较大的$\alpha \ge 0.5$,这远远大于Leaky ReLu和传统ReLu的0.01和0,也就是说在浅层网络中,需要的非线性较弱,此时,正负的激活都很重要。
不过将$\alpha$变成参数也有一定弊端,最明显的是它增加了过拟合的风险。
随机化 ReLu
随机化也是一种解决超参数设定的方法。 随机化ReLu最早是用于Kaggle的一个数据竞赛上。
具体实现上,$\alpha$的取值在训练阶段服从于一个均匀分布,而在测试阶段将其指定为均匀分布所对应的期望。

这个方法也帮助那只队伍在竞赛中一举夺魁。
ELU
ELU, 指数化线性单元,是一个非常年轻的激活函数(出生于2016年)。
它也能够解决死区问题,但是指数运算会增加一些计算量。通常这里的超参数$\alpha$会设为1.
Swish 函数
Google Brain也提出了一个形似ReLu的激活函数, Swish。
其中$\sigma$就是上述的sigmoid函数,$\beta$可以人为设定,也可以训练得到(通常就设为1)。
由于它处处连续可导,而且计算起来不那么麻烦,也拥有和ReLu同样的有点同时一定程度上避免了死区问题。因此在google的论文中,他们宣称Swish函数普遍优于ReLu(及其变体),并且更适用于深层的网络结构。当然这篇论文出来还是有不少争议,有人觉得不过是一篇水文,能够发表不过是因为google的业界影响力,也有人觉得确实有一定贡献。
就实践来看,目前Swish还没有普遍替代ReLu的趋势,还需要更多从理论和实验上来证明Swish函数优点的工作,现在还是等时间检验吧。
选用合适的激活函数
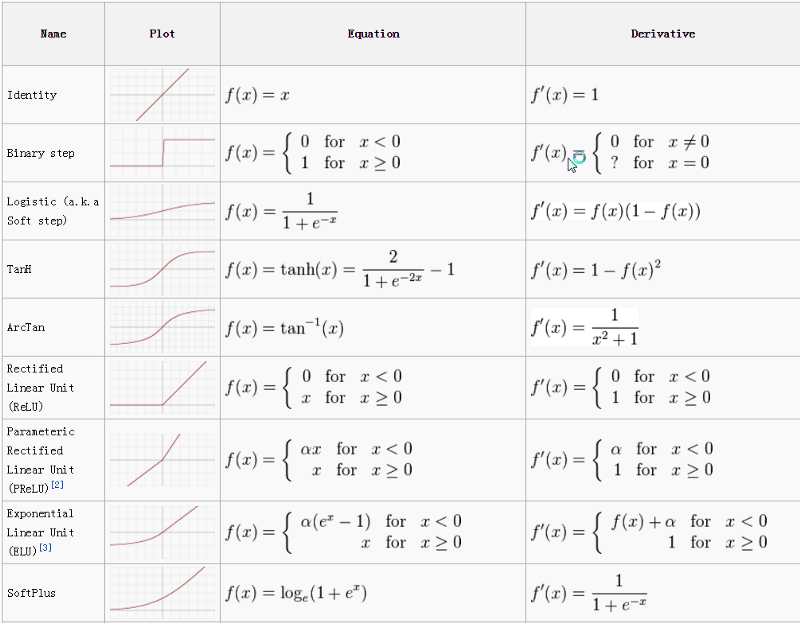
说了这么多激活函数,其实还是可以看出一条清晰的研究脉络的。 最早是用于模拟生物神经元的阶跃函数,但是为了解决不光滑不连续的问题,Sigmoid函数应运而生,而tanh函数则是sigmoid函数的调整值域的变体。 之前的函数都有着梯度消失的问题,因此softplus函数出现了,并由此引入了计算更简单的ReLu函数。其后,由于ReLu的死区问题,各种变体ReLu和Swish函数最终登场。
可以用一张图来总结:
那么我们应该如何选用合适的激活函数呢? (这里我们讨论的是隐藏层的激活函数选用,输出层激活函数的选择通常是基于其预测值类型)
首先要认识到,目前没有一个公认的“最优的”激活函数,不同的激活函数可能在不同类型的数据上做到较好的效果。
其次,由于tanh和sigmoid函数这两个最早的激活函数由于其缺陷现在已经不太使用了,因而我们通常都是用ReLu函数起手。
如果ReLu的效果不好(特别是发现有很多神经元长期失活),然后不妨试试看它的各种变体(新潮点可以选择Swish函数)或是softplus。
最后,如果能够不计时间调参的话,通常为了达到最好效果,可以简单在原来的激活函数上自定义,通常是乘以一个常数的超参数来调节。







