【PRML】第二章 概率分布
概述
对于这一章而言,首先介绍了几种不同的分布,包括二值乃至多值离散的分布以及高斯分布。这类方法统称为参数分布,因为这些分布通过若干个参数(例如高斯分布的方差)就导出整个分布。那么对于这些分布,重要的就是求出这些参数,对于频率学派,我们通过优化某些指标来得到参数,比如使用极大似然函数。对于贝叶斯学派,我们引入基于参数的一个先验分布,然后通过贝叶斯定理和给出的数据来计算后验分布。
一个比较直观的不同是,频率学派在表示要求参数时使用的是$\hat{\theta}$,贝叶斯学派用的是$p(\theta|X)$
这里我们会引入共轭先验的概念,给定似然函数,这个先验会使得后验分布具有和先验类似的函数形式,这会大大地方便贝叶斯分析。需要指出的是,我们通常会说分布a的共轭分布是b,其实是不科学的,更严谨的表述是对于给定形式的后验分布b的某个参数的先验共轭分布是a。我们在说beta分布是伯努利分布的共轭分布时是可以接受的,因为伯努利分布只有一个超参数,但是对于多于一个超参数的分布时这么表达就可能有歧义。
下面先概括下这一章的内容吧。
2.1介绍了二值离散随机变量的一些分布:
- 伯努利分布及用极大似然求伯努利分布参数的方法。
- 二项分布及其期望和方差的表达
- beta分布,指出了beta分布是伯努利分布的共轭分布,并对beta分布的超参数做出了解释
2.2 是多项式变量,这里介绍了多项式分布以及用极大似然+拉格朗日乘子求解多项式分布中参数$\mu$ 的方法。
接着,指出对于参数$\mu$ ,多项式分布的先验分布是Dirchlet分布。而狄利克雷分布中的参数$\alpha_k$是样本分量$x_k=1$的effective number。
2.3节花了很大的篇幅来介绍高斯分布。
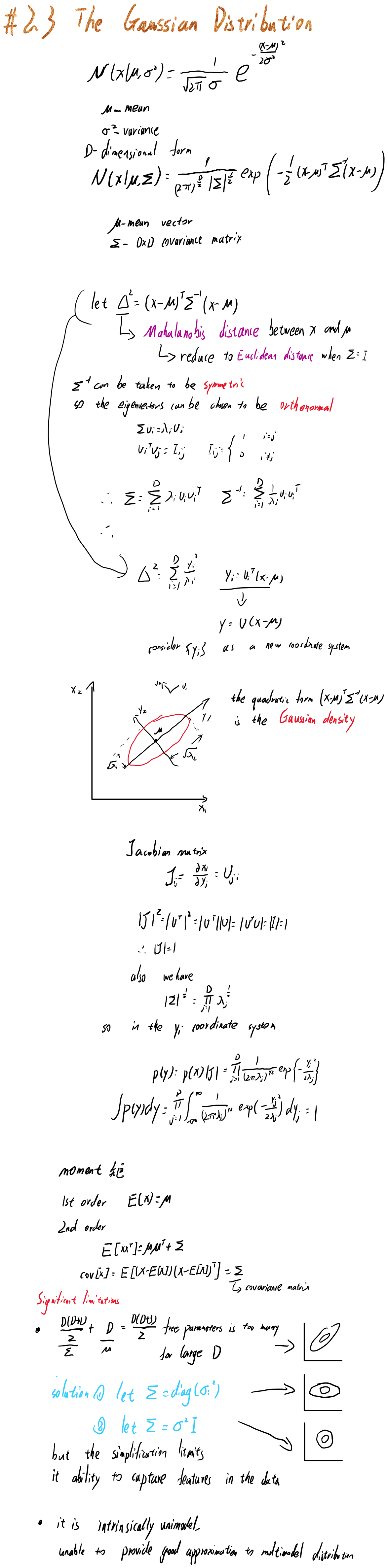
首先给出了高斯分布的单变量和多变量形式,并指出我们研究时需要重点关注的点,概率分布函数中的二次项形式,也就是Mahalanobis distance $(x-\mu)^T\Sigma^{-1}(x-\mu)$ ,这里指出协方差矩阵的逆可以取为对称矩阵,以方便特征向量可以取为正交。特征向量能取正交的话,我们就可以选取一组基,使得该高斯分布在表示上变成标准正态分布。
接下来给出了矩(moment),高斯分布的一阶矩就是期望,二阶矩$E[xx^T]=\mu\mu^T+\Sigma$。
但是这样的高斯分布有着一个很大的缺点,就是参数过多,对于一个协方差矩阵和一个均值向量,有着$D(D+3)/2$ 个参数。所以对应的办法有设协方差矩阵为对角矩阵等。
2.3.1中开始讲条件分布。高斯分布一个重要的性质就是,若两组变量联合分布是高斯分布,那么它一组变量对两一组变量的条件分布和边缘分布都是高斯分布。
确定了条件分布的是高斯分布后,至关重要的就是找到参数,这里引入了一个实用的方法配方法(complete the square)。另外就是用精度矩阵(协方差矩阵的逆)的表示会更简洁。这样我们就能推出条件概率分布的方差和均值。
2.3.2顺势来讲边缘高斯分布。同样的,这里也是用配方法来确定参数。需要注意的是,这里$p(x_a)=\int p(x_a,x_b)dx_b$ 会把$x_b$ 积分掉,所以可以通过配方法给 $x_b$ 配出一个二次型,那么显然这个积分出来就是一个高斯分布正则化系数的倒数,也就是一个常数,那么就可以不用理会了。接着对剩下来的项配方就好。
2.3.3的内容需要和2.3.2的好好甄别其不同,2.3.2是给出给出了了两组变量的联合分布,然后去推其中一组变量的条件概率和边缘概率,而2.3.3是给出了一组变量的边缘概率分布$p(x)$ 和条件概率$p(y|x)$ 去推另一组变量的边缘分布$p(y)$ 和条件概率$p(x|y)$,这里重要的点是通过设$z=(x,y)$ 来推$z$ 的分布,也就是$x,y$ 的联合概率分布。然后用贝叶斯定理来推剩下的值。因此这一节就叫做高斯变量上的贝叶斯定理。
2.3.4来到极大似然估计,这一块和传统的概率论教材比较像,给出了多变量高斯分布的参数极大似然估计。
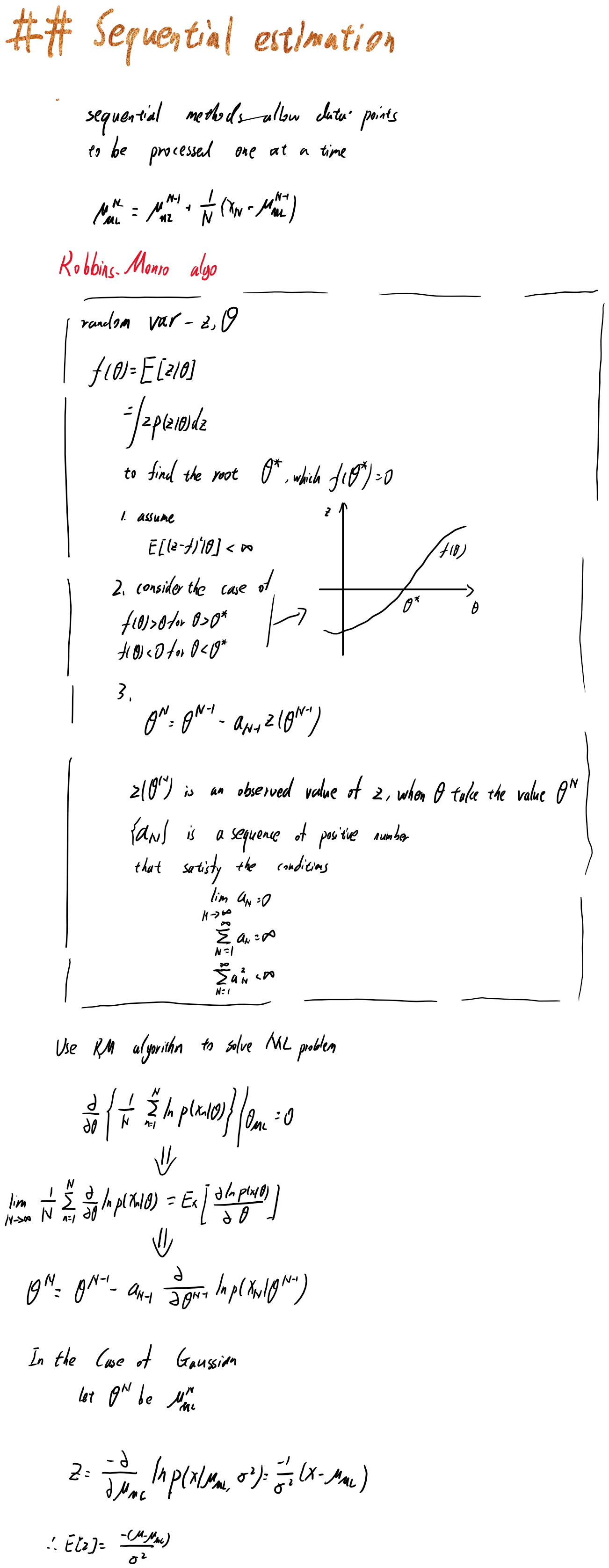
2.3.5是序列估计,当数据过大无法一次处理或者在Online情况下,我们需要通过序列估计来迭代地更新我们对参数的估计。这里用到了Robbins-Monro算法。
2.3.6是高斯分布的贝叶斯推断。这里是贝叶斯学派的确定分布的参数的方法。分别给出了已知方差推均值,已知均值推方差,方差和均值都未知的情况。对于单变量的高斯分布,对其均值的共轭先验分布也是高斯分布,对其方差的共轭先验分布则是Gamma分布,而同时推断均值和方差时,其共轭先验分布是高斯-Gamma分布。类似的,对于多变量高斯分布,当精度矩阵已知时,对其均值的共轭先验是高斯;而均值已知时,对其精度矩阵的共轭先验是Wishart分布。
2.3.7是学生t分布。学生t分布可以由有限个有着相同均值和不同精度的高斯分布叠加得到,当参数$v=1$ 时,该分布退化为Cauchy分布,而$v\rightarrow\infty$ 时则退化为高斯分布。学生t分布相比于高斯分布更加长尾,因此鲁棒性更好,不易受outlier的干扰。
2.3.8说的是周期变量,因为感觉不太涉及到的到,就先放了放没看。
2.3.9是混合高斯分布,混合高斯分布一般指高斯分布的线性组合,组合的权重成为混合因子。对于单变量的混合高斯分布,我们可以通过极大似然去得到一个封闭解析解,但是多变量时,形式会变得非常复制,所以我们无法得到解析解,转而使用EM算法来求解。
2.4 讲了一下指数族分布,将之前提到的很多分布都归纳到这一框架下并提出了它们的一些共性。
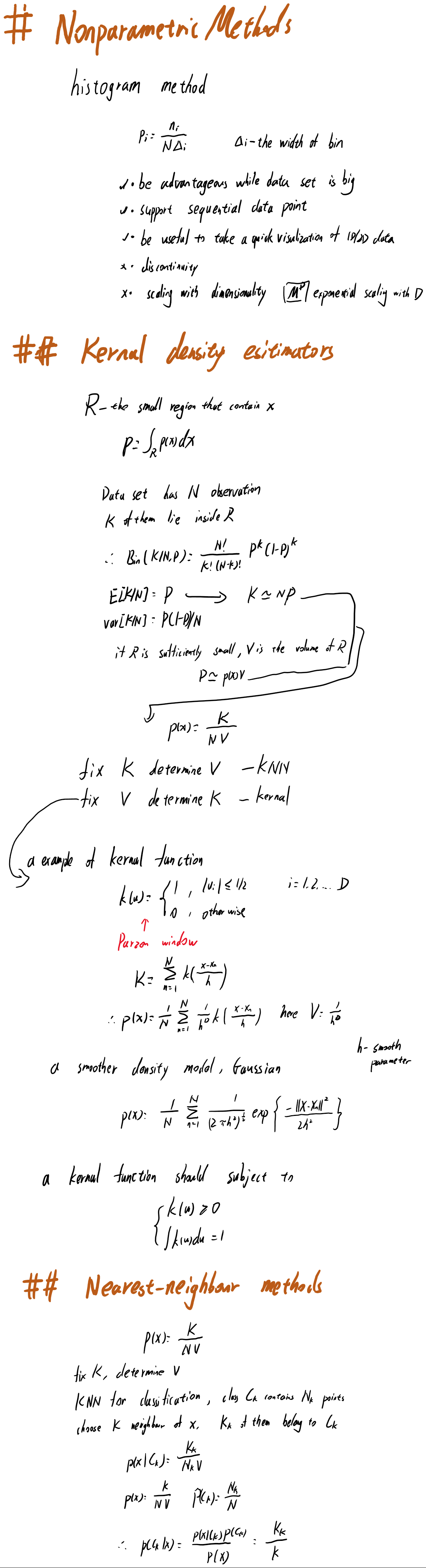
2.5则涉及了一些非参数方法。之前的分布,往往可以由很少(相对数据量来说)的参数来决定,例如高斯分布中的均值方差,但是如果我们没有办法对分布做假设,此时需要让数据自己说话,就需要用到非参数方法。这里首先提到了最基础的histogram法,也就是装桶统计法,然后由 $p(x)=K/NV$ 引申出两类常用的方法,核方法和K近邻法。当然,非参数方法在大量数据时无法很好的应用,因为需要存储所有数据,而且来一个新的数据来计算其概率的计算时间复杂度往往和总数据量成线性增长。因此这类方法还有许多值得探索改进的地方。
下面是详细笔记
2.1 Binary Variable 二值变量

2.2 Multinomal Variable 多项式变量

2.3 The Gaussian Distribution 高斯分布
2.3.1 Conditional Gaussian Distributions 条件高斯分布

2.3.2 Marginal Gaussian Distribution 边缘高斯分布

2.3.3 Bayes’ theorem for Gaussian variables 高斯变量的贝叶斯定理

2.3.4 Maximum likelihood for the Gaussian 高斯分布的极大似然
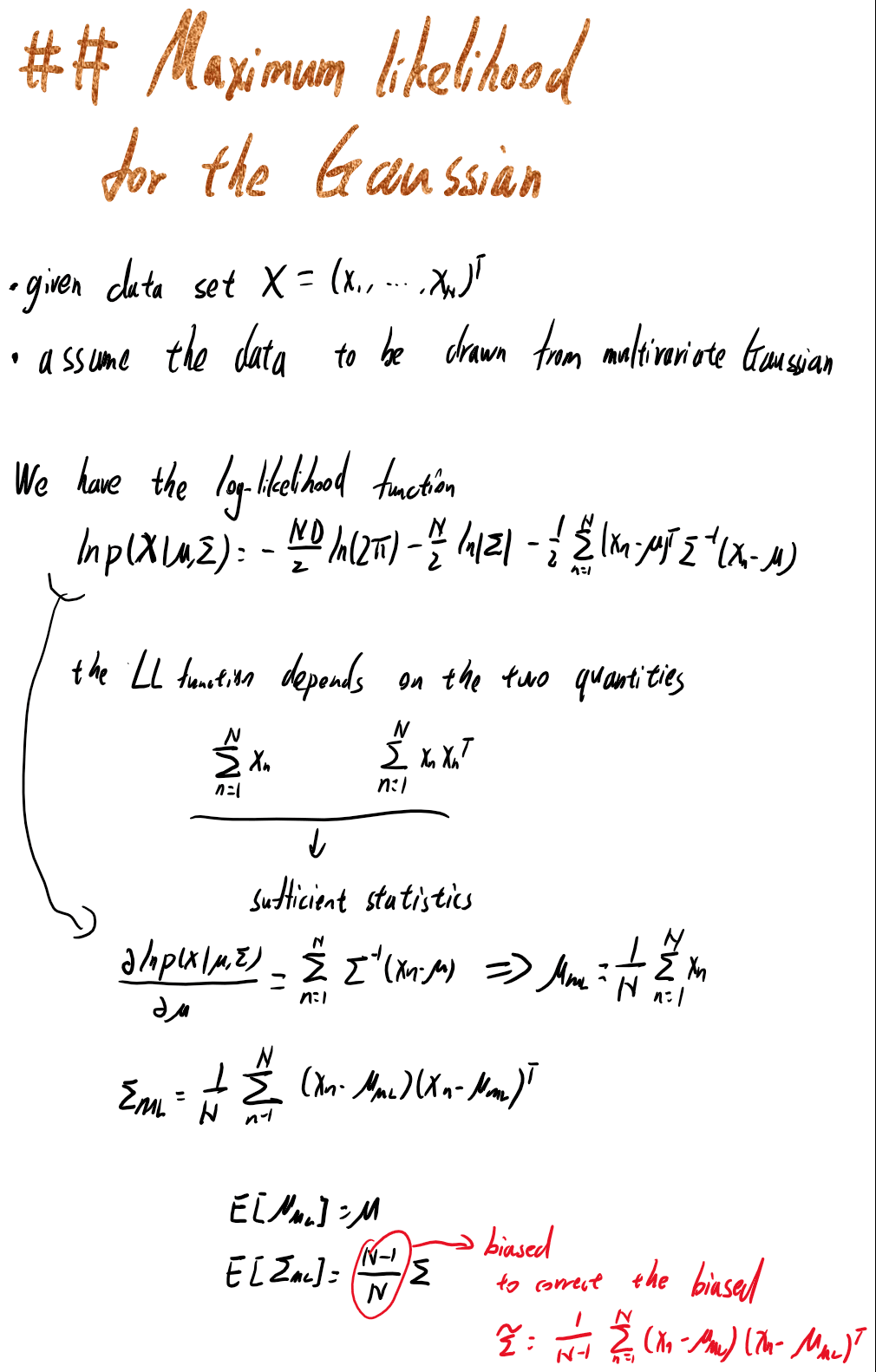
2.3.5 Sequential estimation 序列估计
2.3.6 Bayesian inference for the Gaussian 高斯分布的贝叶斯推断

2.3.7 Students’ t-distribution 学生t分布

2.3.9 Mixtures of Gaussian 混合高斯分布

2.4 The exponential Family 指数族分布

2.5 Nonparametric Methods 非参数方法