梯度下降算法变种及各类优化使用
最近看了一些有关梯度下降的内容，在这里做一下总结，包括梯度下降的变种，学习速率的设定等等，着急的可以拉到最下看结论。
基础梯度下降变种
全批量梯度下降 Batch GD
将全量训练集的样本都计算梯度后再更新，对于有$n$ 个样本的训练集，$\lambda$为学习速率，每次更新参数时如下：
这种方法太过耗时了，而且无法应用在在线算法上，所以一般只有数据量较小时才采用。
随机梯度下降 SGD
和上面的算法相反，SGD是在每计算出一个样本的梯度时就更新参数：
相比较之下，这种算法就可以快很多，但是因为每个样本都会导致参数的立刻更新，当遇到极端样本时，很容易把参数带“跑偏”，表现在损失函数上就是损失函数下降地不稳定，但是往往经过足够多次更新后，算法表现都会稳定下来，当然为了减轻这种不稳定性，使用SGD往往需要将学习速率慢慢降低。
小批量梯度下降 mini-batch GD
这种算法介于BGD和SGD之间，也就是每次通过一个mini-batch的数据来更新参数，一个mini-batch包含$m\in(0,n)$个样本，这个$m$往往会取一个定值（一般在$10^2-10^3$之间），那么相应的，参数的更新就是。
根据Hinton的说法，mini-batch比SGD更优秀，特别是在训练集数据可能有很多重复的时候。取mini-btach size的时候推荐取2的幂，比如128或者256，利于运算优化。
梯度下降算法优化方法
梯度调整相关
Momentum 动量法
当遇到鞍点时，SGD可能浪费很多时间在鞍的两侧徘徊，为了加快速度，可以使用Momentum算法。算法本质就是计算本次梯度时加上一部分上次的梯度，即：
$\gamma$通常设置为0.9或者其他小于1的值，这种方法使得参数在“确认的方向”上前进的更快，而在“犹豫的方向”上减慢下降速度，通常在确认问题有唯一全局最优时非常有效。
Nesterov 加速梯度
但是在Momentum方法中，一个球在按梯度往下滚的时候仅仅是盲目地随着势头，显然这是不够的。Nesterov加速梯度（NAG-Nesterov accelerated gradient）能够给我们的球一点点智能。在使用动量法时，我们知道我们的参数$w$会有一个动量项的变动$\gamma g^k$，那么我们在求偏导的时候就预先将这个变动加上，也就是我们算的不是当前位置的偏导，而是“可预测的未来”的偏导，也就是说我们先按照动量法里上次的梯度走一大步$\gamma g^k$，然后在计算如下的梯度：
也就是不管怎么说，先走一段，然后再打开谷歌地图看下北仑怎么走,It’s better to correct a mistake after you have made it.。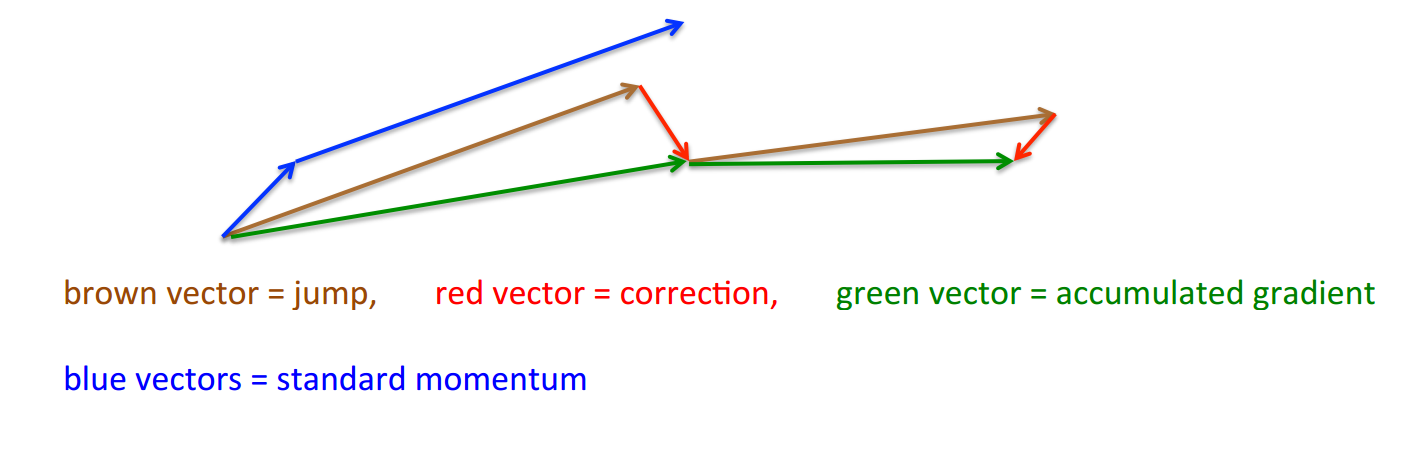
Nesterov
如图所示，蓝色的路线就是Momentum的路径，而Nesterov则是先走一步（棕色路线）再回正（红色路线）。
学习速率相关
下面几种方法都和学习速率相关
Adagrad法
这是一种对不同参数有着不同学习率的算法，基于对那些频繁更新的参数，调低它们的学习速率，对不频繁更新的参数则将其调大的朴素思想，因此对稀疏数据较为适用。谷歌那帮人发现这可以大大提高SGD的鲁棒性。
我们先来考虑单个参数$w_i$在第$t$ 步的情况，$G_{t,i}=\nabla_w l(w_i)$ , 那么按照一般梯度下降$w_{t+1,i}=w_{t,i}-\lambda g_{t,i}$，但是Adagrad这里将学习速率调整为：
这里的 $G_t \in\mathbb{R}^{d\times d}$ 是一个对角矩阵，其对角线上$i,i$ 表示参数$w_i$ 到$t$时的梯度的平方和，$\epsilon$是平滑项，通常设为1e-8。那么向量化后就是：
这里$\odot$是元素逐个相乘。
Adagrad的好处在于我们不用手动调学习速率了，其缺点在于我们总是在学习率的分母上累计平方和，因此学习率会越来越小，过分小之后会导致梯度消失等问题（不恰当的初始化参数也会导致这个问题）。下面的Adadelta就旨在修复这一问题。
Adadelta
Adadelta是Adagrad的一种改进（从名字上也能猜出来），首先在累计梯度平方和的时候，该算法不会将从头开始的梯度一直累加，而是使用衰减平均累加，我们用$E[g^2] $来表示，那么$E[g^2]_t=\gamma E[g^2]_{t-1}+(1-\gamma)g_t^2 $
这里$\gamma$就像是动量法里面那样，也是一个小于1的数值（约0.9）。那么我们就有
分母就是方均根(root mean square RMS)，所以$\sqrt{E[g^2]_t+\epsilon}$ 也可以简写为 $RMS[g]_t$。
更进一步的，Adadelta的作者发现，更新公式中没有直接对应参数更新的单位，然后由Hessian方法推导出一阶近似Hessian方法（分母上加了参数的）。具体推导可以看原文。最终就得到了Adadelta的终极版本：
这里$RMS[\Delta w]_t=\sqrt{\gamma E[\Delta w^2]_{t-1}+(1-\gamma)\Delta w^2_t}$，而$\Delta w_t= -\frac{RMS[\Delta w]_{t-1}}{RMS[g]_t}g_t$ 。其实也就是这里分子上用一个和参数有关的猜测单元(hypothetical units)来替代了固定值学习率（初始化的时候$E[g^2]_0=0$，$E[\Delta x^2]_0$=0)。也就是说我们彻底消灭了一个超参数——学习速率。
但是该算法也是有缺陷的，其最大缺陷就在于在训练后期无法脱离局部最小值吸引盆（这时候可以考虑加上动量法）。
RMSprop
这个算法其实本质上和Adadelta差不多，是Hinton独立于Adadelta发现的，其更新策略就等同于上述Adadelta的中间版本。
这里$\lambda$可以默认为0.001。
Adam
Adaptive Moment Estimation(Adam)是另一种为每个参数计算不同学习速率的方法，即存储了梯度平方的指数衰减平均（和Adagrad一样），也存储了梯度本身的指数衰减平均：$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$ ,$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$ （$m,t$都初始化为0），但是作者发现他们都容易偏移到0，特别是衰减速率较小的情况下（$\beta$很接近1）。
为此，他们提出要修正这种偏移：
$\hat{m}_t = \frac{m_t}{1 - \beta^t_1} $，
$\hat{v}_t = \frac{v_t}{1 - \beta^t_2} $
最终的更新策略就是
其他方法
重排 和 Curriculum Learning（课程学习）
简单来说就是每次迭代后对训练集样本进行重排，防止每次迭代式batch都一样。
而课程学习是有深度学习大牛Bengio在09年的ICML上提出，后来Koller在10年的NIPS上进一步模型化，简单说就是将学习目标进行由易到难的排列，协助算法跳出局部最优。
在这里的应用就是将训练集样本也进行由易到难的排列（比如人脸识别中，先喂人脸没有遮掩的样本，然后再喂比如带口罩/面纱/眼镜的样本）。
提前停止
在训练过程中监视误差变化，在改进停滞后停止训练。
加入梯度噪声
就是指在梯度更新中加入一个噪声值，一般是一个服从高斯分布的随机值，往往加入噪声项之后利于模型跳出局部极小。
小结
| 方法 | 思想 | 优点 | 局限 |
|---|---|---|---|
| 动量法 | 加速下降（梯度不是下降的原因而是改变下降状态的原因，类比于力学） | 加快训练速度，在只有唯一全局最优时很好用 | 太过于盲目，往往加速过头 |
| Nesterov加速度 | 在动量法基础上先走一段再回正 | 相较动量法更加“智能” | 回正有时适得其反 |
| Adagrad | 区别对待频繁更新的参数和很少更新的参数 | 在稀疏数据上表现好，增强鲁棒性，不用手动调学习率 | 可能导致学习率过小而致的梯度消失 |
| Adadelta | 改进adagrad，二阶方法的一阶近似 | Adagrad的优点且克服缺点再加上完全摆脱了超参数学习速率 | 训练后期难以脱离局部最小值吸引盆 |
| RMSprop | 根据参数分量最近的平均梯度量级改变学习率 | 和Adadelta类似 | 实际效果上略逊完全版的Adadelta |
| Adam | 使用梯度的一阶和二阶指数衰减平均 | 收敛速度快，不易陷入局部最小 | 需要鲁棒的初始化 |
总的来说，Adam和Adadelta应该是最好用的两类优化，值得首选，并在此基础上加入其他算法试试。
总的来说我们分两种情况来看，首先是小数据集（10,000）或者是大量的无重复数据集：
wechat
alipay
