无监督学习 Unsupervised Learning

聚类 Clustering K-means算法

步骤

  1. 先根据簇数选出K个聚类中心(cluster centroids)
  2. 进行迭代，每次迭代时将
    　a) 先每个样本标签为离它最近的聚类中心。
    　b) 计算有共同标签的样本的中心值作为新的聚类中心替代原来的。如果某个聚类中心在迭代后没有依附其上的样本，那么通常会选择删除这个聚类中心，我们就得到K-1个簇。如果要保持簇集数不变，那么也可以保留它到下面的迭代。
  3. 迭代终止后得到结果。

优化目标

假设：
$c^{i}$-第i个样本的簇标号
$\mu_k$-第k个簇的聚类中心
$\mu_{c^{i}}$第i个样本所在簇的聚类中心
那么：
$J=\frac{1}{m}\sum^m_{i=1}||x^i-\mu_{c^{i}}||^2$
有点像Supervisor Learining中的cost function
优化目标就是最小化J（又称失真代价函数Distortion cost function）。。

初始化

如何初始化聚类中心：较为推荐的方法是在训练集中随机挑选K个样本作为聚类中心。多次初始化并执行K-means算法来避免陷入局部最优。

选择K

簇聚类个数的选择往往模棱两可，这里我们可以使用下面的方法。
肘部法则((Elbow method)
选择不同的簇聚类数，计算出J，画出折线图，选择J畸变较为明显的点(Elbow)作为簇聚类数。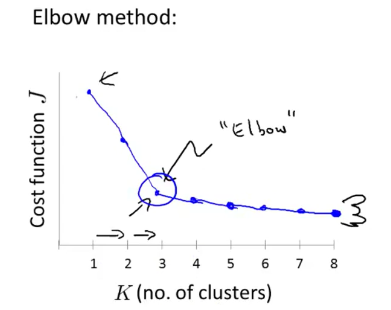
QQ图片20160305153304.png-37.2kBQQ图片20160305153304.png-37.2kB
但是这个方法常常不管用，因为肘点往往也不清晰。(╬ﾟдﾟ)

维数约简 Dimensionlity Reduction

数据压缩

  • 将相同的但是以不同形式(进制/单位/幂次)呈现的特征量降到一维，即取其中一个。
  • 对于n个特征量，若数据能够基本上分布在一个超平面上，那么可以将数据投影到这个平面，从而从n维降到n-1维。

    数据可视化

    因为我们眼睛只能看到3维的图像，所以将数据降维才能实现数据可视化。

    PCA算法(Principal Component Analysis)

简述

寻找一个超平面(低原特征空间一个维度的平面)，将数据投影上去，并调整超平面到数据投影和原数据点的距离最小。

步骤
  1. 通常先进行均值归一(mean normalization)，特征缩放(feature scaling).。
  2. 求出协方差矩阵(covariance matrix)并算出其特征向量(eigenvectors)。
    $协方差矩阵=\frac{1}{m}\sum^n_{i=}(x^i)(x^i)^T$
  3. 取出特征向量U的k列，称为$U_{reduce}$,$z=U_{reduce}’*x$,则z即为降维后的数据。

    数据还原

    $x_{approx}=U’*z$ 会有数据损失。

    如何选择K

    K既是主成成分(PC)的数量。
    我们要计算成分的差异性，即降维前后的差异，一般用$\frac{\sum||x^i-x^i_approx||^2}{\sum||x^i||^2}$表示。这个值低于某个阈值比如1%时。
    从k=1开始，应用PCA算法并计算差异性，满足要求即取该值，否则增加k。
    差异性除了上面的计算方法还可以用求U时的调用svd函数得到的S矩阵求解。
    (svd的具体实现和原理忘了，因为线性代数已经忘得差不多了，等过一阵子复习一下线代再补。)
    $1-\frac{\sum_{i=1}^kS_{ii}}{\sum_{i=1}^nS_{ii}}$

    心得

    PCA算法实质上只是一个降维算法，将数据从高维进行低维，并尽量保持原数据的特点。数据压缩后可以提高学习算法的处理速度。
    但是在ISLR中还利用PCA来实现clustering，一般是降维到超平面，并利用超平面将数据分成若干类。