Coursera Machine Learning Lunar’s note

异常检测 Anomaly detection

高斯分布 Gaussian Distrubution

又叫正太正态分布Normal Distrubution。
对于$x\in \Re$,如果期望为$\mu$，方差为$\sigma^2$,那么我们就可以称，$x\sim \aleph(\mu,\sigma^2)$(读作x服从mu和sigma的高斯分布)。
维基百科维基百科
该分布的概率分布曲线像是山丘，以$x=\mu$对称，山丘的陡峭程度和
相关，$\sigma$越小，曲线越陡峭。

参数估计

对于给定的数据集，如果认为该数据分布符合正态分布，那么可以对他们进行参数估计，即利用数据集的分布情况来估算正态分布的参数($\mu和\sigma$)。
$\mu = \frac{1}{m}\Sigma^m_{i=1}x^i$
$\sigma^2 = \frac{1}{m}\Sigma^m_{i=1}(x^i-\mu)^2$
ps.概率论课上这两个公式的分母都是$m-1$但是在机器学习领域更通用m，虽然在数学理论上二者不同，但是实际应用中差别很小。

算法

首先，我们要算出某个样本的估算密度，对于有n个特征值的样本x，
$p(x)=\Pi_{i=1}^n p(x_i,\mu_i,\sigma^2_i)=\Pi_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma_i}exp(-\frac{(x_i-\mu_j)^2}{2\sigma_j^2})$。
下面是具体算法步骤

  1. 选择出有利于检测出异常的特征值。
  2. 对于给出的无标签数据集，计算出正态分布的参数。
  3. 对于新的样本，计算出$p(x)$，当小于阈值时($p(x)<\varepsilon$)，判定为异常。

    算法的评估

    通过带标签的数据，我们可以用数字量化对算法的评估。
    假定CV集和测试集都是带标签的，而训练集是不带标签的数据。
    在训练结束后，我们通过CV集/测试集的数据计算出评估量：
  • 真/假 阴/阳 值
  • 召回率/查准率
  • $F_1-值$
    关于这些值的含义在Week6有提及。
    选择 $\epsilon$ 值通常通过CV集中的F-score值来判断。

    监督学习 vs. 异常检测

    |异常检测|监督学习|
    |—-|—-|
    |正负样本数量相差非常悬殊，有一项非常小|正负样本数量都很大|
    |异常的类型多样（但数量不一定多），难以预料|训练集样本异常包含大多数或几乎所有的异常类型，且类型数较少|
    | 欺诈检测|垃圾邮件分类|
    |生产检测|天气预测|
    |机器故障检测|癌症诊断|

    特征值选择

  • 高斯化
    对于分布看起来不像正态分布的特征量，我们可以通过转换，比如log运算使其分布更加贴合高斯分布。

  • 特征值
    选择更加能够区分正常样本和异常样本的特征值。

    改进：多元高斯分布

    以上的异常检测不能兼顾到特征值之间的联系。比如网站用户检测，每月登陆1次可能是正常的，每月消费10笔也可能是正常的，但是如果同一用户每月只登陆一次但是消费10笔，那么可能就是异常的，然而以上的检测并不会考虑这个。当然我们可以通过增加二者的比率（每次登陆消费笔数）来解决，但是当特征值较多时，就无法如此简单的解决。所以我们引入多元高斯分布。
    对于$\mu \in \Re^n,\Sigma \in \Re^{n*n}$,
    $p(x;\mu,\Sigma)=\frac{1}{(2\pi)^{n/2}|\Sigma|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu))$
    这里$\Sigma$是个n*n的矩阵，$|\Sigma|$是该矩阵的行列式的值。
    利用如下公式进行参数拟合
    $\mu = \frac{1}{m}\Sigma^m_{i=1}x^i \quad \Sigma = \frac{1}{m}\Sigma^m_{i=1}(x^i-\mu)(x^i-\mu)^T$。
    接下来对example，计算$p(x)$并和阈值比较。
    如果数据含有重复特征值或者冗余（线性相关）特征值(如$x_1=x_2\qquad x_3=x_1+x_2$)，那么协方差矩阵$\Sigma$会是不可逆的，也就不能使用多元高斯模型（m>n时也不能用）。

    推荐系统 Recommender System

    基于内容的推荐

    设置基于内容的特征量，值越大表示包含该特征内容越多。比如($x_1(romance)$)，那么一部电影的$x_1$表示该电影的爱情片成分有多少。将用户看过的电影的基于内容的特征值作为输入X，评分作为输出y，那么我们可以通过回归算法拟合每个用户的参数，并通过此对用户未评分的电影进行评级。

    协同过滤 Collaborative Filtering

    不同于上面基于内容的推荐，这里我们不事先对电影的内容提取特征值，相反，我们对用户的喜好提取特征值。
    如：用户对爱情电影的喜好为5，对动作电影的喜好为1。那么大量搜集这些信息后就可以结合用户给不同电影的评分，得到电影的内容特征值。
    我们可以看出，前面是通过电影内容特征估计用户喜好特征，后面是通过用户喜好特征来估计电影内容特征，这两种方法可以结合起来：

  • 具体算法
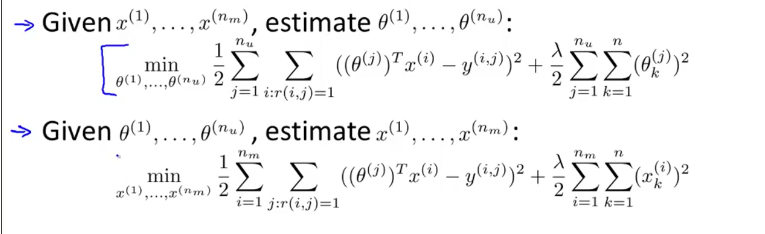    Collaborative filtering.png-66kBCollaborative filtering.png-66kB
    我们将其统一起来，其评估函数加起来形成一个新的评估函数$J(x^1…x^m,\theta^1…\theta^u)$,最小化$J$。

  • 步骤
  1. 初始化$x^1…x^m,\theta^1…\theta^u$
  2. 利用梯度下降最小化$J$，不断更新参数。
  3. 对于每个用户和每个电影可以估算出评分值。
  • 向量化实现
    将用户对各个电影的评分可以用矩阵表示。$Y^{ij}$表示用户j对电影i的评分。那么就有$Y=X\Theta^T$,$\Theta$是各个用户的特征值；$X$是电影的特征矩阵，每行为一部电影的各个特征。