猴子也能理解的EM算法

这个例子来自Do, Chuong B, and Serafim Batzoglou; 2008; What Is the Expectation Maximization Algorithm? Nature Biotechnology 26(8): 897–899.

EM算法是ML中一种非常重要的参数估计方法, 在很多地方都用应用. 上述论文给出了一种EM算法的非常直观而又不失精要的理解方式.

抛硬币游戏

假设这样一个抛硬币的测试, 我们有两个硬币A和B, 它们正面朝上的概率分别为$\theta_A$和$\theta_B$, 我们重复以下操作五次:

从AB中随机抽一个硬币
抛该硬币10次并记录结果

接着我们需要从这个实验中得到对$\theta_A$和$\theta_B$的估计.

极大似然估计

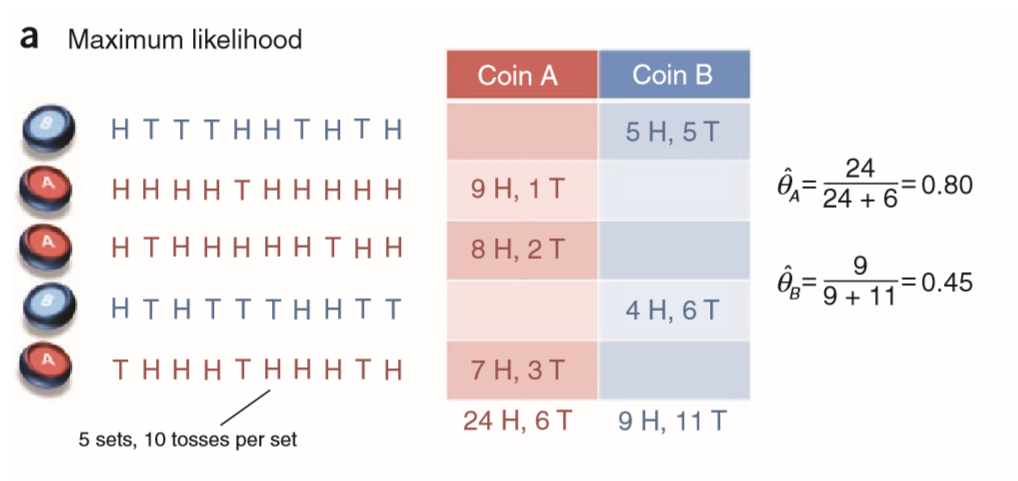
假设我们的试验结果如上图, 那么我们很容易用极大似然估计来预测:

$\begin{array}{l}{\hat{\theta}_{A}=\frac{24}{24+6}=0.80} \\ {\hat{\theta}_{B}=\frac{9}{9+11}=0.45}\end{array}$

具体来说, 我们不妨假设, 实验的五次操作中, 每次操作正面朝上的次数为$xi$, 那么有变量$x=(x{1}, x{2}, \ldots, x{5})$.
同时, 令$zi$为每次操作时选择硬币的类别(A or B), 则有$z=(z{1}, z{2}, \ldots, z{5})$, 那么极大似然估计就是列出这些参数的联合概率分布$\log P(x, z ; \theta)$,并求其最大化的参数$\hat{\theta}=\left(\hat{\theta}{A}, \hat{\theta}{B}\right)$.
其实二项式分布+极大似然估计然后就看得到这个公式:

$\begin{array}{c}{\hat{\theta}_{A}=\frac{\# \text { of heads using coin } \mathrm{A}}{\text { total } \# \text { of flips using coin } \mathrm{A}}} \\ {\hat{\theta}_{B}=\frac{\# \text { of heads using coin } \mathrm{B}}{\text { total } \# \text { of flips using coin } \mathrm{B}}}\end{array}$

如果到这里结束那也就没有EM什么事了, 现在来给这个游戏加点难度. 现在假设我们不知道每次操作的时候我们抛的到底是硬币A还是B, 也就是说, 变量$z$变得不可观测了(hidden variable). 此时我们常称$z$为隐变量(hidden variable / latent factor). 这种情况在参数估计中叫做不完全数据. 此时我们就无法直接用极大似然估计来估算概率了, 为此就有了EM算法.

EM算法

如上所述, 我们的问题变成了不完全数据下的参数估计, 那么一个简单的想法就是将这种不完全数据给补全了, 那我们的问题不就可以归结到完全数据的参数估计了嘛.

于是, 一种很简单的迭代式的想法就是:

先初始化参数$\hat{\theta}^{(t)}=(\hat{\theta}{A}^{(t)}, \hat{\theta}{B}^{(t)})$
对测试中每次操作, 基于现有的参数猜想它是由A还是B抛出的.
根据上一步的猜想, 我们将不完全的数据补全了, 此时就可以用极大似然估计来更新参数$\hat{\theta}^{(t+1)}$.
重复前两步步骤直到收敛.

其实到这里, EM算法的大概思路就已经出来了. 第三步中的问题其实就是上一节所介绍的, 那么重点就在于第二步中我们如何猜想. 实际上EM算法基于现有的参数$\hat{\theta}^{(t)}$来对缺失数据(隐变量)的每种可能都计算出概率值, 然后用这种概率对所有可能的补全数据加权. 最后我们的极大似然就基于这种调整了权重的训练样本.

下面我们举个例子说明一下: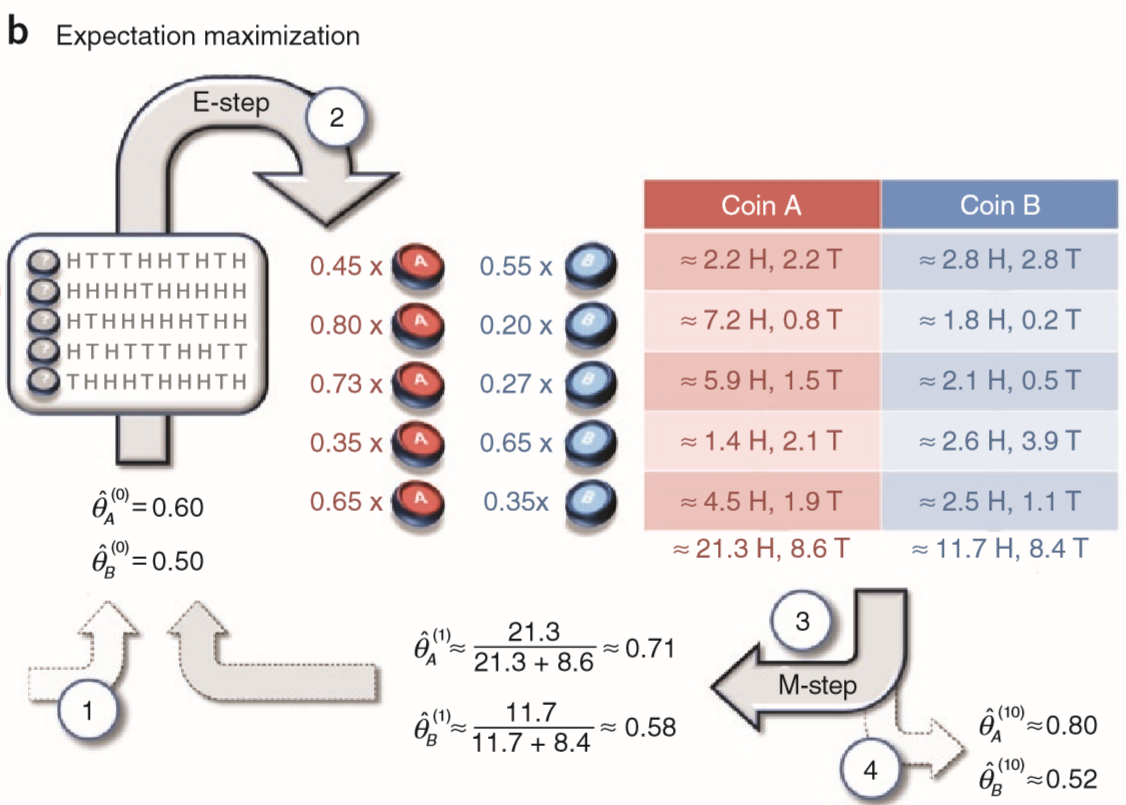

在上图中, 我们按步骤标号来解释:

初始化参数 $\hat{\theta}{A}^{(0)}=0.60$ , $\hat{\theta}{B}^{(0)}=0.50$ .
E-step, 我们对缺失的数据进行补全. 例如对于第一次操作, $z_1=A$的概率为0.45, 而$z_1=B$的概率为0.55. 其他四次实验样本也是类似的操作, 然后我们就得到右边这样一个调整了权重的训练样本.
M-step, 基于上面的数据用极大似然估计来更新参数.
重复上述两步若干次到收敛后, 输出结果.

在上面的步骤中E-step得名于Expectation(期望), 其实也就是我们通常没必要显示计算出数据补全的概率分布, 而只需要计算期望的显著统计量. 而M-step得名于Maximization, 也就是这一步会去最大化期望的对数似然.

令人生畏的数学基础

对大部分人来说, 上面的部分就已经足够了, 但是对好奇心过剩的人们来说, 不妨看看下面简单的数学分析.

我们先回到最初的设定, 即用极大似然解决的完全数据问题, 此时我们的目标函数$\log P(x, z ; \theta)$有一个全局最优点, 也就是说该问题通常有一个解析解.

与之相反的是, 在不完全数据的情况下, 目标函数$\log P(x ; \theta)$有多个局部最优而没有闭式解.

为了解决这个问题, EM算法的做法将这个困难的优化问题化解为一系列更简单的子问题, 具体而言, 这些子问题都有一个全局最优且有闭式解, 而这些依次解决的子问题的解$\hat{\theta}^{(1)}, \hat{\theta}^{(2)}, \ldots$保证会收敛于原问题的一个局部最优.

在E-step中, 算法选择了一个函数 $gt$ 作为目标函数$\log P(x;\theta)$的下界, 也就是$g{t}(\hat{\theta}^{(t)})=\log P(x ; \hat{\theta}^{(t)})$. 而在M-step中, 算法就针对最大化$g_t$函数选择了一个新的参数$\hat{\theta^{(t+1)}}$. 因为我们的下界函数$g_t$对应了参数为 $\hat{\theta^{(t)}}$时的目标函数, 我们也就有

$\log P\left(x ; \hat{\theta}^{(t)}\right)=g_{t}\left(\hat{\theta}^{(t)}\right) \leq g_{t}\left(\hat{\theta}^{(t+1)}\right)=\log P\left(x ; \hat{\theta}^{(t+1)}\right)$

那么我们的目标函数也就能在迭代中不断下降直到收敛于局部最优. 为了避免局部最优, 我们通常会以不同的初始点多次进行EM算法来打破模型的对称性, 并选择其中最优的结果.

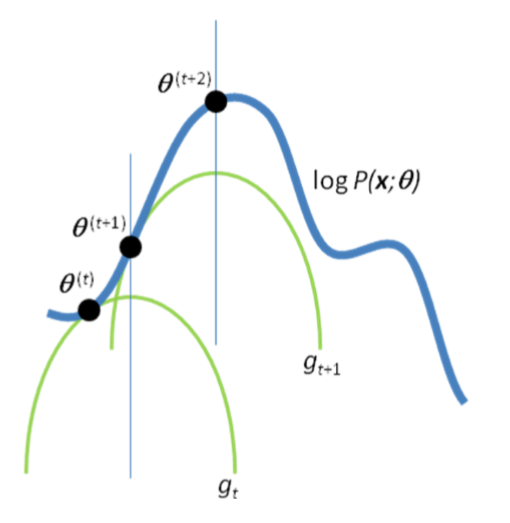
上图给出了EM算法的一个直观图示, 蓝线是真实的目标函数, 一条条绿线则是不断逼近局部最优的下界函数.